Алгоритм определения параметров
Перепишем систему линейных уравнений (6.7) в виде
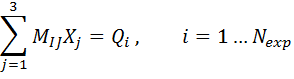
(6.8)
Эта система переопределена, так как количество уравнений 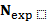 больше количества неизвестных. В общем случае она не имеет решения, так как экспериментальные данные неизбежно содержат случайные ошибки и, кроме того, сама модель, связывающую эти данные условием (6.5), достаточно приближенной. Поэтому целесообразно искать решение X, которое наилучшим образом приближает левые и правые части равенств (6.8). Метод наименьших квадратов приводит к системе трех уравнений с тремя неизвестными
больше количества неизвестных. В общем случае она не имеет решения, так как экспериментальные данные неизбежно содержат случайные ошибки и, кроме того, сама модель, связывающую эти данные условием (6.5), достаточно приближенной. Поэтому целесообразно искать решение X, которое наилучшим образом приближает левые и правые части равенств (6.8). Метод наименьших квадратов приводит к системе трех уравнений с тремя неизвестными
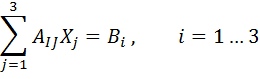
(6.9)
где матрица и вектор правой части (6.9) имеют вид:
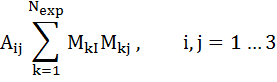
, (6.10)
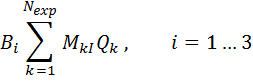
Решение системы (6.10) выходит через обратную матрицу
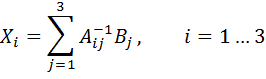
(6.11)
что дает нам значения искомых параметров In(A),U и ∆V.
С полученным таким образом решением находим дисперсию отклонений теоретических значений от экспериментальных
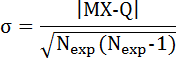
(6.12)
Величина ơ показывает для каждого объекта совпадение теории с экспериментом.
Качество подгонки решение характеризует также величина обусловленности системы уравнений, которая, как известно, равна произведению Евклидовых норм прямой и обратной матрицы системы (6.10),
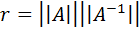
(6.13)
где
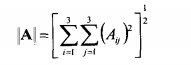 (6.14)
(6.14)
числа обусловленности r показывают чувствительность решения системы линейных уравнений к погрешности в определении матричных элементов.
Вопросы для самоконтроля
1.Как действие времени выдержки отличается от эффектов влияния и давления, и температуры?
2.Как увеличение времени обработки изменяет порог полной стерилизации микроорганизмов? Как при этом меняется концентрация витамина С?
3.Как увеличение температуры обработки изменяет порог полной стерилизации МАФАМ? Как при этом меняется концентрация витамина С?
4.Как повышение давления обработки влияет на время достижения полной стерилизации? Как при этом меняется концентрация витамина С?
5.Как увеличение температуры обработки при постоянном давлении влияет на концентрацию микроорганизмов и витамина С?
6.Какая комбинация давления Р, температуры Т и срока обработки и однозначно определяет величину концентрации?
Задачи и примеры
1.На основе данных табл. 4.2 с помощью решения кинетического уравнения (6.3) найти константу скорости деградации витамина С в вишневом соке под влиянием термообработки при нормальном давлении.
2.На основе данных табл. 4.2 с помощью решения кинетического уравнения (6.3) найти разбег констант скорости деградации витамина С в вишневом соке под влиянием термообработки при нормальном давлении.
7.ПРИМЕРЫ РАСЧЕТОВ ТЕРМОДИНАМИЧЕСКИХ ПАРАМЕТРОВ
Результаты расчетов на примере вишневого сока
Для более точного определения термодинамических параметров в работе [4] были проведены детальные экспериментальные исследования влияния давления Р, температуры Т и времени выдержки t в содержание витамина С, МАФАМ и плесени в вишневом соке. Общее количество точек во всех трех сериях опытов для каждого исследуемого объекта воздействия (витамин С, МАФАМ, плесень - таблицы А.2-А.10) с учетом всех повторений составляет 72.
Результаты решения переопределены системы (6.7) методом наименьших квадратов и представлены в табл. 7.1, где А измеряется в обратных секундах, ơ-дисперсия отклонений теории от эксперимента, r - обусловленность найденного решения, равная произведению Евклидовых норм прямой и обратной матрицы системы линейных уравнений метода наименьших квадратов. Если полученные значения дисперсии ơ можно считать вполне удовлетворительными, то обусловленность r, что определяет чувствительность полученного решения к случайным ошибкам, получилась довольно большая для всех исследуемых объектов. Иначе говоря, получаемые в этой модели термодинамические параметры могут содержать непредсказуемую ошибку. Причина такой высокой чувствительности кроется в физике процесса, согласно которой реакция среды связана двойным потенцированием с изменением параметров системы (6.4). Исправить эту ситуацию нельзя в принципе, можно только двигаться в направлении стандартизации условий опыта и накопления экспериментальных точек. Так для отделения неучтенных эффектов среды может быть предложена концепция модельных экспериментов, в которых пищевая среда имитируется буферным раствором с заданным рН [9].
Таблица7.1 Термодинамические параметры процессов деградации витамина С и инактивации микроорганизмов в вишневом соке.
| Объект | In(A•1сек) | U,ккал⁄моль | ∆V,мл⁄моль | ơ | r |
| Витамин C | 12,03 | 12,4 | -3,61 | 0,02 | |
| МАФАМ | 13,52 | 15,9 | -35,5 | 0,08 | |
| Плесень | 7,91 | 12,9 | -38,7 | 0,08 |
Косвенным подтверждением правильности полученных параметров может служить близость изменений молярного объема ∆V МАФАМ и плесени (табл. 7.1) к известным характерных значений для разных белков (табл. 7.2). Полученное изменение молярного объема ∆V для небольшой молекулы витамина С по модулю на порядок меньше, чем характерные значения этого параметра для микроорганизмов (табл. 7.1) или для белков (табл. 7.2), что представляется вполне разумным. Обращает на себя внимание близость изменения энергии U для всех трех объектов характерной величины энергии разрушение водородных связей (~11 ккал / моль). Дальнейший анализ причин такого совпадения может привести к пониманию природы молекулярных конформаций, которые лежат в основе как деградации витамина С, так и инактивации микроорганизмов.
Таблица 7.2 Наблюдаемые изменения объема белков при денатурации под давлением (по данным: Prehoda K.E.та др. [14])| Белок | ∆V(мл⁄ 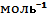 ) )
|
| Ribonuclease A | -6, -46, -56 |
| Staphylococcal Nuclease | -85 |
| Chymotrypsinogen | -14 |
| Lysozyme | -26 |
| Metmyoglobin | -60 |
| Flavodoxins | -64 |
| FMN - binding protein | -74 |
На рисунках 7.1, 7.2 и 7.3 подано кривые, рассчитанные с использованием найденных параметров, по сравнению с экспериментальными данными.
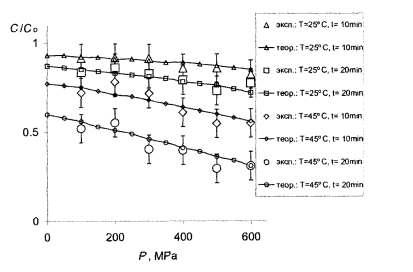 Рис.7.1- Сравнение теории с опытом для витамина C . Большие маркеры – эксперимент (табл.4.3), кривые с мелкими маркерами - расчет в тех же условиях с параметрами с табл.7.1.
Рис.7.1- Сравнение теории с опытом для витамина C . Большие маркеры – эксперимент (табл.4.3), кривые с мелкими маркерами - расчет в тех же условиях с параметрами с табл.7.1. 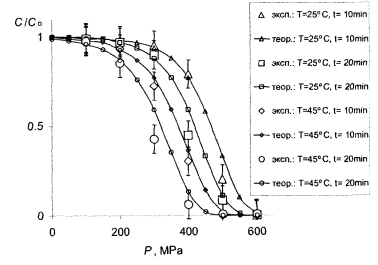
Рис.7.2 - Сравнение теории с опытом для МАФАМ. Большие маркеры-эксперимент (табл.4.4), кривые с мелкими маркерами-расчет при тех же условиях с параметрами с табл.7.1
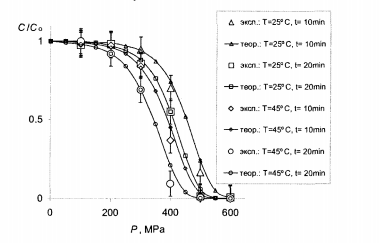
Видно, что в целом теория вполне удовлетворяет этот эксперимент. В частности, кривые передают правильный ход концентрации в зависимости от давления как для витамина С, так и для МАФАМ и плесени, а также правильно отражают тенденции изменения этих зависимостей при изменении температуры и времени обработки. В рамках одной и той же формулы получаются как плавно спадающие почти линейные зависимости для витамина С, приведены на рис. 7.1, так и ступенчатые кривые для МАФАМ на рис. 7.2 и плесени на рис. 7.3.
Сравнивая ход кривой денатурации под давлением на рис. 3.7 с кривыми инактивации микроорганизмов на рис. 7.2 и 7.3 можно заметить корреляцию между степенью инактивации микроорганизмов и степенью денатурации белков. Кроме того, значение термодинамических параметров для различных белков (табл. 7.2) по порядку величины совпадают с найденными в работе значениями (табл. 7.1). Все это подтверждает предположение о химической природе процесса инактивации и позволяет считать денатурацию белков ключевым звеном механизма инактивации микроорганизмов [2].
Результаты расчетов на примере яблочного пюре
Для того, чтобы планировать эксперимент или технологию обработки высоким давлением неизученных объектов, необходимо выяснить насколько и почему меняются при изменении среды параметры, описывающие инактивацию той или иной группы микроорганизмов, например, МАФАМ. С этой целью [6] было исследовано влияние высокого давления на содержание микроорганизмов группы МАФАМ в яблочном пюре, приготовленном из свежих яблок непосредственно перед опытами [2].
Для описания кинетики инактивации было найдено: предэкспоненциальгый множитель А, активационный барьер реакции U и изменение объема ∆V, входящих в уравнение Аррениуса (5.14) для константы скорости реакции. Эти параметры определялись [2] по данным табл. 4.6 путем решения методом наименьших квадратов переопределены системы уравнений (6.7) (ơ = 0,09, r = 5500). Найденные значения параметров приведены в табл. 7.3. Как видно из таблицы, параметры для случая яблочного пюре [2] близки к результатам, полученным для вишневого сока. Обращает на себя внимание небольшое уменьшение активационного барьера U и выигрыша молярного объема -∆V.
Таблица 7.3 - Сравнение параметров инактивации МАФАМ в различных средах
| Объект | In(A•1c) | U, ккал / моль | ∆V, мл / моль |
| МАФАМ в яблочном пюре | 13,2 | 13,4 | -25,1 |
| МАФАМ в вишневом соке | 13,5 | 15,9 | -35,5 |
На рис. 7.4 представлены результаты сравнения экспериментальных и расчетных относительных чисел КУО МАФАМ для случаев Т = 30°С, t = 20мин (серия 1) и T = 25°С, t = 10 мин (серия 2), полученных для яблочного пюре, а также кривые, рассчитанные по данным [4] для вишневого сока.
Из рисунка видно, что вполне удовлетворительно согласуется теория с опытом для обеих серий, а также, что в обоих случаях является заметный сдвиг в сторону меньших давлений (примерно на 150 МПа) относительно кривых для вишневого сока. Как следует из анализа табл. 7.3 рис. 7.4, небольшие сдвиги параметров приводят к заметным различиям расчетных кривых, связано с двойным потенцированием этих сдвигов.
Необходимо отметить, что набор параметров (InA, U, ∆V) дает приближенное усредненное описание процесса инактивации целой группы микроорганизмов, существенно различаются по чувствительности к давлению. Это возможно только в том случае, если в основе инактивации лежит некий общий для всех микроорганизмов процесс. Возможно, таким процессом является денатурация белков под давлением[4]. Процессы денатурации и выживаемость микроорганизмов в общем, при прочих равных условиях, определяются, прежде всего, кислотностью среды. Хорошо известно, что скорость инактивации микроорганизмов давлением растет со снижением рН [59]. В связи с этим наблюдаемые сдвиги кривых в сторону меньших давлений обусловлен, очевидно, различными значениями кислотности в яблочном пюре (рН = 5,3) и в вишневом соке (рН = 6,1)
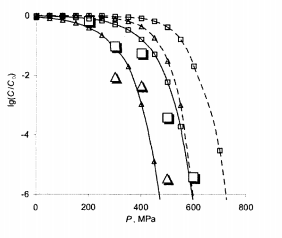
Рис.7.4 -Логарифм относительных чисел КУО МАФАМ зависимо от давления P при разных температурах T и временем обработки t, большие маркеры – эксперимент [69], кривые с маркерами – расчет при тем же условиях, сплошные линии – яблочное пюре, пунктирные – вишневый сок:
▲-T=30°C, t=20 мин; ■-T=25°C, t=10 мин.
Таким образом показано, что набор параметров (InA, U, ∆V), описывающих кинетику инактивации микроорганизмов, можно использовать для оценки влияния высокого давления на микроорганизмы в различных средах с учетом изменения кислотности. Для сред с меньшими рН таким способом можно получить оценку сверху, а для сред с большими рН - оценку снизу. Величины давления 400 и 500 МПа являются критическими для полной стерилизации яблочного пюре при Т = 30°С, t= 20 мин и Т = 25°С, t = 10 мин соответственно.
Расчет параметров инактивации спор
Bacillus subtilis и Bacillus stefrothermophilus
Полученные выше результаты могут быть использованы для выбора оптимальных параметров обработки и создают предпосылки для разработки отсутствующих в данный момент стандартов технологии обработки продуктов питания сверхвысоким давлением. Однако с точки зрения биофизики высоких давлений остается неясным, насколько широкий класс объектов, для каких применима используемая модель, будет ли она описывать известны данные по инактивации микроорганизмов, полученные в работах других авторов. Чтобы ответить на этот вопрос, разработана методика была использована [4] интерпретации данных с инактивации спор Bacillus subtilis [87] и Bacillus stearothermopgilus [88].
В работе [87] споры Bacillus stearothermopgilus АТСС 9372 инкубировались сутки в аэрированных стандартном питательной бульоне при 37°С. Дkя спорулизации эта культура высевалась на питательный агар с добавлением 10 мг/л МnSО4 и 500 мг/л МnSО4. После семидневной инкубации при 37°С споры сбивали в суспензию, фильтровали, трижды центрифугировали по 45 мин. при 5500 об/мин и 4°С, окончательно разводили в стерильном 0,9% растворе NaCI и доводили концентрацию до 107-108спор/мл. В таком виде споры хранились при 4°С до одного месяца с неизменной концентрацией. Обработка давлением осуществлялась двумя независимыми способами: с быстрым (5-30 с) и медленным (2,5-20 мин) ростом давления. После обработки образцов давлением из них готовились серии десятикратных разведенных, которые высевались на питательный агар в тройной повторности. Чашки с агаром инкубировались сутки при 37°С, после чего количество спор выживших подсчитывалось по средним числами КУО/мл.
В работе [70] споры Bacillus stefrothermophilus АТСС 7953 с исходной концентрацией примерно 2•108 КУО мл-1были инкубированные в течение 24 часов в стандартном питательном бульоне при 55°С. В конце инкубационного периода 3 мл суспензии равномерно распределены по поверхности чашек Петри с питательным агаром, содержащих 10 мг/л MnS. После 4-5 дней инкубации при температуре 55 °С оценивалась доля спор клеток с помощью метода фазовой микроскопии. Когда 90% клеток были со спорами, инкубация заканчивалась. Споры и вегетативные клетки разделялись центрифугированием при 5000 оборотах в течение 20 минут с последующей обработкой 70% Etoh и повторным центрифугированием при 5000 оборотах в течение 20 минут. Наконец, полученные таблетки снова размешивались в стерильной дистиллированной воде и замораживались до -20°С, что обеспечивало постоянную концентрацию спор в течение всего периода хранения. образцы подвергшихся воздействию в широком диапазоне давлений от 200 до 1400 МПа и температур от 90 до 130°C. Изучение инактивации выполнялось в фосфат буферном растворе с рН = 7,0. После обработки готовились серии разведенных образцов, которые по два повтора высевали на стандартный питательный агар. Количество клеток, выживших определялась после 48 часов инкубации при 37°С.
Для получения параметров инактивации спор Bacillus subtilis были использованы табличные данные [87], полученные в случае быстрого роста давления. Для спор Bacillus stefrothermophilus набор точек было восстановлено по отдельным графикам на рис. 3.2, 3.3 c [88]. Эти данные с выживаемости спор под давлением были обработаны по методике, изложенной ранее (тема 6). Полученные в результате значение термодинамических параметров приведены в табл. 7.4. Там же указано значение дисперсии ơ обусловленности решение r и число уравнений 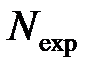 в системе (6.7), решаемой методом наименьших квадратов. Для сравнения в табл 7.4 приведены также полученные ранее параметры инактивации для некоторых вегетативных форм микроорганизмов.
в системе (6.7), решаемой методом наименьших квадратов. Для сравнения в табл 7.4 приведены также полученные ранее параметры инактивации для некоторых вегетативных форм микроорганизмов.
Таблица 7.4 - Параметры инактивации спор Bacillus subtilis и Bacillus stearothermophilus по сравнению с результатами для вегетативных форм с табл. 7.1 и 7.3
| Объект | In(A•1c) | U, ккал / моль | ∆V мл / моль | ơ | r | 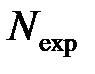
|
| Споры Bacillus subtilis | 17,34 | 15,57 | -9,97 | 0,02 | ||
| Споры Bacillus stearothermophilus | 18,57 | 17,84 | -9,18 | 0,05 | ||
| МАФАМ в вишневом соке [4] | 13,52 | 15,90 | -35,5 | 0,08 | ||
| МАФАМ в яблочном пюре [2] | 13,18 | 13,44 | -25,11 | 0,09 | ||
| Плесень в вишневом соке [41 | 7,91 | 12,91 | -38,7 | 0,08 |
На рис. 7.5, 7.6 рассчитанные с этими параметрами теоретические кривые, сравниваются с усредненными по разным повторенностям экспериментальных данных. В общем наблюдается вполне удовлетворительное согласие. Теоретические кривые правильно передают как масштабы изменения концентраций под давлением, так и тенденции, связанные с изменением температуры и времени обработки. Из-за большого разброса экспериментальных данных некоторые точки не попали в отраженные участки концентраций. Таким образом, возможности модели не ограничиваются вегетативными формами.
Как видно из табл. 7.4, значения активационного барьера U оказываются примерно одинаковыми для всех объектов. Можно предположить, что это та самая величина и, следовательно, активационный барьер инактивации различных микроорганизмов определяется тем самым процессом, не связанным с их размером, массой или формою.
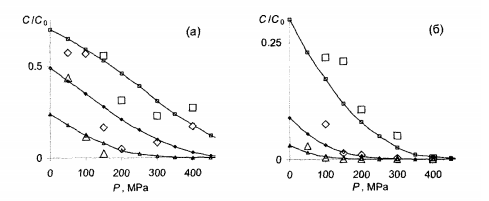
Рис. 7.5 – Выживание спор Bacillus subtilis в зависимости от давления P при различных температурах T и срока обработки t, большие маркеры – эксперимент [69], кривые с маркерами – расчеты при тех же условиях:
а) T = 30 °C, □ – t = 30, ◊ - t = 60 и ∆ - t = 120 мин;
б) T = 60 °C, □ – t = 10, ◊ - t = 20 и∆ - t = 30 мин.
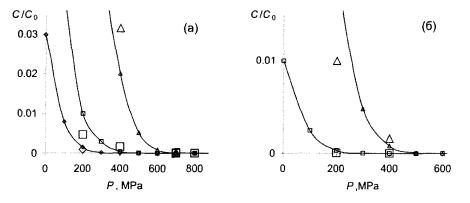
Рис. 7.6 - Выживание спор Bacillus subtilis в зависимости от давления P при различных температурах T и срока обработки t, большие маркеры – эксперимент [70], кривые с маркерами – расчеты при тех же условиях:
а) T = 100 °C, ∆ – t = 5, □ - t = 10 , ◊ - t = 15 мин;
б) T = 110 °C, ∆ – t = 5, □ - t = 10 мин.
Как известно, значение свободной энергии стабилизации различных белков также разбросаны в достаточно узком интервале (от 10 до 20 ккал/моль) [150] и явно не зависят от размеров белка.
Приведенные в табл. 7.4 значения энергии активации U попадают в указанный интервал для энергий стабилизации, представляется довольно странным, и заставляют думать, что те же события на микроскопическом уровне ответственные как за стабилизацию структуры белков по распаду N → D, так и при переходе в активированное состояние N → 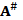 , с которого происходит спонтанная денатурация
, с которого происходит спонтанная денатурация 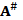 → D
→ D
Значение изменения удельного объема ∆V для всех объектов табл. 7.4 по порядку величины совпадают с характерными значениями ∆V для белков (табл. 7.2), что подтверждает предположение о том, что инактивация микроорганизмов обусловлена деградацией белков [4, 2]. Величины ∆V для различных вегетативных форм вышли примерно одинаковыми. То же самое можно сказать о спорах, причем ∆V для спор заметно меньше, чем для вегетативных форм. Это еще одно подтверждение связи инактивации микроорганизмов с деградацией белков, поскольку в спорах белки упакованы более плотно, у них отсутствуют или минимизированы полости, заполняемые водой при развертывании.
Это наблюдение дает нам еще один довод в пользу того, что образование активированного состояния перед денатурацией белка N → 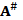 связано с открытием доступа воды во внутренние полости белка, поскольку заполнения их водой дает основной вклад в уменьшение объема. После заполнения полостей становятся возможными макроперемещения пептидных цепей, что, по сути, и является денатурацией. Объем на этом этапе
связано с открытием доступа воды во внутренние полости белка, поскольку заполнения их водой дает основной вклад в уменьшение объема. После заполнения полостей становятся возможными макроперемещения пептидных цепей, что, по сути, и является денатурацией. Объем на этом этапе 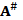 → D не меняется, поэтому изменение объема ∆V при активации промежуточного состояния N →
→ D не меняется, поэтому изменение объема ∆V при активации промежуточного состояния N → 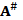 оказывается равным изменению объема для равновесной реакции N → D (см. рис. 5.2).
оказывается равным изменению объема для равновесной реакции N → D (см. рис. 5.2).
Проведенный анализ позволит нам в дальнейшем сделать выводы о микроскопических процессах, с которыми связана инактивация микроорганизмов давлением (см. тему 10).
Вопросы для самоконтроля
1.Как меняется объем белков при денатурации под давлением?
2.Какие наблюдения подтверждают предположение о химической природе процесса инактивации и позволяют считать денатурацию белков ключевым звеном механизма инактивации микроорганизмов?
3.Как соотносятся параметры инактивации спор Bacillus subtilis и Bacillus stearothermophilus по сравнению с результатами для вегетативных форм?
Задачи и примеры
1.С помощью графиков на рис. 7.5 определить параметры обработки, необходимо применить для стерилизации образцов со спорами . Bacillus subtilis.
2.С помощью графиков на рис. 7.6 определить параметры обработки, необходимо применить для стерилизации образцов со спорами Bacillus stearothermophilus.
3.Сравните рисунки 7.2 и 7.3 и сделайте выводы о смещении порогов инактивации при росте температуры или срока обработки.
Дата добавления: 2021-09-25; просмотров: 777;











