Выбор полуреплик. Генерирующие соотношения и определяющие контрасты
При построении полуреплики 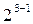 существует всего две возможности: приравнять х3 к +х1х2 или к — х1х2. Поэтому есть только две полуреплики
существует всего две возможности: приравнять х3 к +х1х2 или к — х1х2. Поэтому есть только две полуреплики 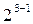 (таблица 1.13).
(таблица 1.13).
Таблица 1.13 – Две полуреплики 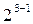
| Номер Опыта | x3 = x1x2 | Номер опыта | x3 = -x1x2 | ||||||
| x1 | x2 | x3 | x1x2x3 | x1 | x2 | x3 | x1x2x3 | ||
| + | + | + | + | + | + | - | - | ||
| - | - | + | + | - | - | - | - | ||
| + | - | - | + | + | - | + | - | ||
| - | + | - | + | - | + | + | - |
Для произведения трех столбцов матрицы I выполняется соотношение: +1=x1x2x3, а матрицы II: -1=x1x2x3. Вы видите, что все знаки столбцов произведений одинаковы и в первом случае равны плюс единице, а во втором — минус единице.
Символическое обозначение произведения столбцов, равного +1 или —1, называется определяющим контрастом. Контраст помогает определять смешанные эффекты. Для того чтобы определить, какой эффект смешан с данным, нужно помножить обе части определяющего контраста на столбец, соответствующий данному эффекту. Так, если 1=x1x2x3, то для x1 имеем 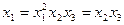 , так как всегда
, так как всегда 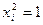 .
.
Для х2 находим 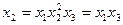 , для х3 находим
, для х3 находим 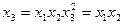 .
.
Это значит, что коэффициенты линейного уравнения будут оценками
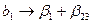 ;
; 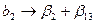 ;
; 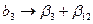 .
.
Соотношение, показывающее, с каким из эффектов смешан данный эффект, называется генерирующим соотношением.
Полуреплики, в которых основные эффекты смешаны с двухфакторными взаимодействиями, носят название планов с разрешающей способностью III(3) (по наибольшему числу факторов в определяющем контрасте). Такие планы принято обозначать: 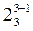 .
.
При выборе полуреплики 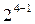 возможно восемь решений:
возможно восемь решений:
1) x4= x1x2, 4) x4= -x2x3, 7) x4= x1x2x3,
2) x4= -x1x2, 5) x4= x1x3, 8) x4= -x1x2x3.
3) X4= x2x3, 6) x4= -x1x3,
Разрешающая способность этих полуреплик различна. Так, редлики 1—6 имеют по три фактора в определяющем контрасте, а 7—8 по четыре. Реплики 7 и 8 имеют максимальную разрешающую способность и называются главными. Разрешающая способность задается системой смешивания данной реплики. Она будет максимальной, если линейные эффекты смешаны с эффектами взаимодействия наибольшего возможного порядка.
При отсутствии априорной информации об эффектах взаимодействия экспериментатор стремится выбрать реплику с наибольшей разрешающей способностью, так как тройные взаимодействия обычно менее важны, чем парные. Если существует информация об эффектах взаимодействия, то она должна использоваться при выборе реплики.
Реплики, в которых нет ни одного главного эффекта, смешанного с другим главным эффектом или парным взаимодействием, а все парные взаимодействия смешаны друг с другом, носят название планов с разрешающей способностью IV(4) (по наибольшему числу факторов в определяющем контрасте). Они имеют обозначение 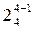 . Полуреплика, заданная определяющим контрастом 1=+x1x2x3x4 имеет только четные комбинации букв в каждой строке. Ее можно записать следующим образом, считая строку (1) четной:
. Полуреплика, заданная определяющим контрастом 1=+x1x2x3x4 имеет только четные комбинации букв в каждой строке. Ее можно записать следующим образом, считая строку (1) четной:
(1), ad, bd, ab, ас, cd, bc, abcd.
А полуреплика, заданная 1= -x1x2x3x4 имеет только нечетные комбинации
а, b, с, d, abd, acd, abc, bcd.
Такие полуреплики называют главными полурепликами, так как они обладают наибольшей разрешающей способностью.
Пусть выбраны полуреплики, заданные определяющими контрастами 1=+x1x2x3x4 и 1= -x1x2x3x4. Совместные оценки здесь определяются соотношениями:
x1 = x2x3x4, x1x3 = x2x4, x3 = -x1x2x4, x1x4 = -x2x3.
x2 = x1x3x4, x1x4 = x2x3, x4 = -x1x2x3,
x3 = x1x2x4, x1 = -x2x3x4, x1x2 = -x3x4,
x4 = x1x2x3, x2 = -x1x3x4, x1x3 = -x2x4,
Такой тип смешивания дает возможность оценивать линейные эффекты совместно с эффектами взаимодействий второго порядка, а взаимодействия первого порядка — совместно друг с другом. Если полуреплики заданы генерирующими соотношениями x4 = x1x2 и x4 = -x1x2, то в этом случае определяющими контрастами являются 1=+x1x2x4 и 1= -x1x2x4, следовательно, мы получаем планы с разрешающей способностью III и некоторые основные эффекты смешиваем с парными взаимодействиями:
x1 = x2x4, x2x3 = x1x3x4, x3 = -x1x2x3x4,
x2 = x1x4, x3x4 = x1x2x3, x4 = -x1x2,
x3 = x1x2x3x4, x1 = -x2x4, x1x3 = -x2x3x4,
x4 = x1x2, x2 = = -x1x4, x2x3 = -x1x3x4,
x1x3 = x2x3x4, x3x4 = -x1x2x3.
Разрешающая способность этих полуреплик ниже, чем у планов с разрешающей способностью IV, с помощью которых линейные эффекты определяются независимо от парных взаимодействий.
Эти полуреплики имеют в каждой строке как четные, так и нечетные комбинации букв. Такие полуреплики не являются главными. Разумен выбор такой полуреплики, если имеется априорная информация о большей значимости тройных взаимодействий по сравнению с парными или о незначимости трех парных взаимодействий x2x4, x1x4, х1х2.
Как видим, выбор дробной реплики требует много терпенья и труда. Но другого пути нет. Применяя дробное планирование, нужно точно знать систему смешивания, четко представлять, какую информацию приходится терять.
Теперь рассмотрим пример полуреплики 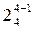 . В качестве факторов рассматривались переменные, показанные в таблице 1.14. Матрица планирования представляла собой полуреплику от
. В качестве факторов рассматривались переменные, показанные в таблице 1.14. Матрица планирования представляла собой полуреплику от 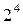 , заданную генерирующим соотношением x4=x1x2x3. Определяющим контрастом является 1=x1x2x3x4. Умножая определяющий контраст последовательно на х1, х2, х3 и х4, определяем совместно оценки линейных эффектов и взаимодействий
, заданную генерирующим соотношением x4=x1x2x3. Определяющим контрастом является 1=x1x2x3x4. Умножая определяющий контраст последовательно на х1, х2, х3 и х4, определяем совместно оценки линейных эффектов и взаимодействий
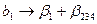 ,
, 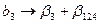 ,
, 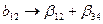 ,
,
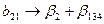 ,
, 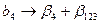 ,
, 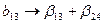 ,
, 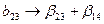 .
.
Таблица 1.14 – Уровни факторов и интервалы варьирования
| Факторы | Уровни факторов | Интервал варьирования | ||
| -1 | +1 | |||
| x1 | ||||
| x2 | ||||
| x3 | ||||
| x4 |
Матрица планирования, результаты эксперимента и коэффициенты регрессии показаны в таблице 1.15.
Таблица 1.15 – Матрица планирования 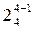
| Номер опыта | x0 | x1 | x2 | x3 | x4 | x1x2= x3x4 | x1x3= x2x4 | x2x3= x1x4 | y |
| + | + | + | - | - | + | - | - | ||
| + | - | - | - | - | + | + | + | ||
| + | + | - | - | + | - | - | + | ||
| + | - | + | - | + | - | + | - | ||
| + | + | + | + | + | + | + | + | ||
| + | - | - | + | + | + | - | - | ||
| + | + | - | + | - | - | + | - | ||
| + | - | + | + | - | - | - | + | ||
| bi | 15,5 | -1,5 | 4,75 | 0,75 | 4,5 | -0,75 | 0,75 | 2,0 |
При выборе полуреплики 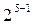 в распоряжении экспериментатора имеется множество вариантов. Так, х5 можно приравнять к одному из шести парных взаимодействий. В этом случае получим полуреплику с разрешающей способностью III. Очевидно, это будет не лучший выбор полуреплики. Далее, х5 можно приравнять к одному из четырех тройных взаимодействий. Тогда получим план с разрешающей способностью IV, и все линейные эффекты будут смешаны с тройными взаимодействиями.
в распоряжении экспериментатора имеется множество вариантов. Так, х5 можно приравнять к одному из шести парных взаимодействий. В этом случае получим полуреплику с разрешающей способностью III. Очевидно, это будет не лучший выбор полуреплики. Далее, х5 можно приравнять к одному из четырех тройных взаимодействий. Тогда получим план с разрешающей способностью IV, и все линейные эффекты будут смешаны с тройными взаимодействиями.
И, наконец, полуреплика может быть задана генерирующими соотношениями x5 = x1x2x3x4 или x5 = x1x2x3x4. Определяющими контрастами в этом случае будут 1 = x1x2x3x4x5 и 1= -x1x2x3x4x5. Такие реплики носят название планов с разрешающей способностью У и обозначаются 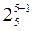 .
.
Дата добавления: 2021-11-16; просмотров: 683;











