Алгоритм решения параметрической задачи включает 3 этапа.
1) Решается обычная задача расстановки судов по линиям (симплекс-методом или модифицированным распределительным методом) для Qj.
2) Определяются значения Zij, т. е. количество флота, необходимого для освоения дополнительного объёма перевозок Bj.
- Сначала определяются значения Zij в столбцах где xij > 0- единственное по столбцу. В этих случаях Zij будет со знаком “+”; если xij = Фi, тогда Zij будет равно 0; если xij < Фi, то Zij > 0.
- Затем переходим к столбцам, где xij > 0 – не единственное в столбце. Здесь могут иметь место 2 случая: если 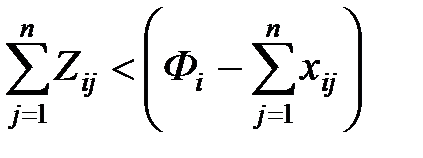 , то Z будет со знаком “+”; если
, то Z будет со знаком “+”; если 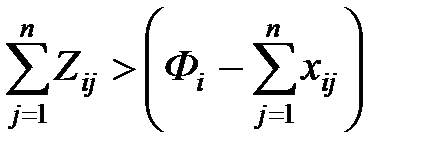 , то Z < 0 .
, то Z < 0 .
3) Находим 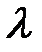 по тем клеткам, где
по тем клеткам, где 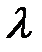 *Zij вычитается:
*Zij вычитается:
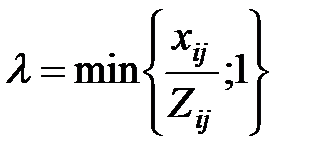
Рассмотрим реализацию алгоритма на примере:
Имеются 4 типа судна и 6 линий движения. До заполнения матрицы должна быть расписана обычная математическая постановка задачи расстановки флота по линиям. Все расчёты будем проводить в матрице
| j | |||||||||
| i | Qj Фi | 130+ 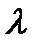 13 13
| 20+ 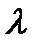 5 5
| 190+ 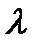 20 20
| 50+ 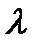 8 8
| 100+ 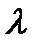 10 10
| 150+ 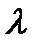 10 10
| Резерв флота | |
2,36+ 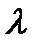 0,23 0,23
|
0,64- 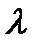 0,43 0,43
|
2+ 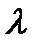 0,2 0,2
| |||||||
1,35+ 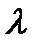 1,01 1,01
|
0,65- 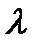 1,01 1,01
| ||||||||
1,11+ 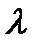 0,28 0,28
|
4,25+ 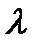 1,51 1,51
|
1,64- 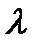 1,79 1,79
| |||||||
3,6- 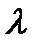 0,6 0,6
|
0,4+ 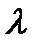 0,6 0,6
|
Z11 = 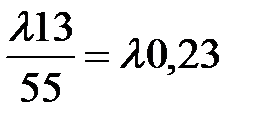
Z32 = 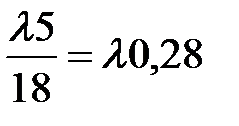
Z15 = 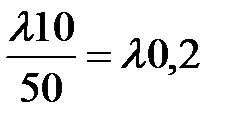
Z14 = l*0,2 + l*0,23 = l*0,43 Z44 = 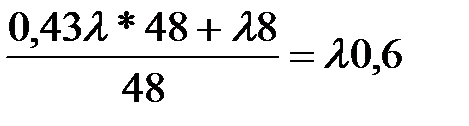
Z43 = - 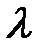 0,6 Z23 =
0,6 Z23 = 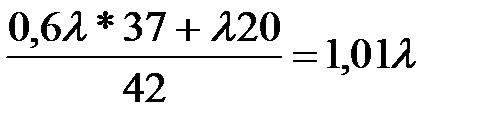
Z26 = - 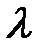 1,01
1,01
Z36 = 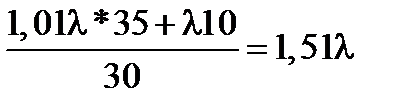
Находим 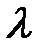 по тем клеткам, где
по тем клеткам, где 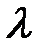 Zij имеет знак « - ».
Zij имеет знак « - ».
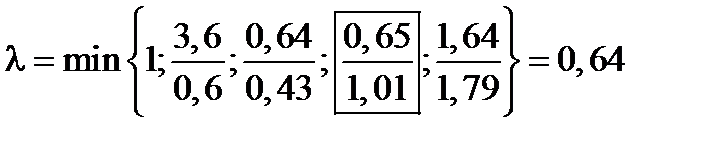
Т. о. на первом этапе мы определили xij, на втором - Zij, на третьем - 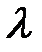
После получения решения необходимо рассчитать значение целевой функции и осуществить проверку ограничений.
Дата добавления: 2019-12-09; просмотров: 959;











