Минимизация числа опытов
Начнем с самого простого — полного факторного эксперимента 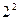 . Напишем еще раз эту хорошо нам известную матрицу (таблица 1.11).
. Напишем еще раз эту хорошо нам известную матрицу (таблица 1.11).
Таблица 1.11 – Полный факторный эксперимент 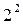
| Номер опыта | x0 | x1 | x2 | (x3) x1x2 | y | Номер опыта | x0 | x1 | x2 | (x3) x1x2 | y |
| + | - | - | + | y1 | + | - | + | - | y3 | ||
| + | + | - | - | y2 | + | + | + | + | y4 |
Пользуясь таким планированием, можно вычислить четыре коэффициента и представить результаты эксперимента в виде неполного квадратного уравнения
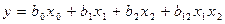 .
.
Если имеются основания считать, что в выбранных интервалах варьирования процесс может быть описан линейной моделью, то достаточно определить три коэффициента; bо, b1 и b2. Остается одна степень свободы. Употребим ее для минимизации числа опытов. При линейном приближении 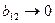 и вектор-столбец х1х2 можно использовать для нового фактора х3. Поставим этот фактор в скобках над взаимодействием х1х2 и посмотрим, каковы будут оценки коэффициентов. Здесь уже не будет тех раздельных оценок, которые мы имели в полном факторном эксперименте
и вектор-столбец х1х2 можно использовать для нового фактора х3. Поставим этот фактор в скобках над взаимодействием х1х2 и посмотрим, каковы будут оценки коэффициентов. Здесь уже не будет тех раздельных оценок, которые мы имели в полном факторном эксперименте 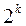 . Оценки смешаются следующим образом:
. Оценки смешаются следующим образом:
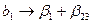 ;
; 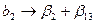 ;
; 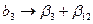 .
.
Но нас это не должно огорчать. Ведь мы постулируем линейную модель, и, следовательно, все парные взаимодействия незначимы. Главное, мы нашли средство минимизировать число опытов: вместо восьми опытов для изучения трех факторов оказывается можно поставить четыре. При этом матрица планирования не теряет своих оптимальных свойств (ортогональность, ротатабельность и т. п.), в чем вы можете самостоятельно убедиться. Найденное правило можно сформулировать так: чтобы сократить число опытов, нужно новому фактору присвоить вектор-столбец матрицы, принадлежащий взаимодействию, которым можно пренебречь. Тогда значение нового фактора в условиях опытов определяется знаками этого столбца.
Какая из трех матриц (рисунок 1.19), предложенных взамен полного факторного эксперимента 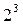 , требующего восьми опытов, больше всего подходит к качестве матрицы планирования для дробного факторного эксперимента?
, требующего восьми опытов, больше всего подходит к качестве матрицы планирования для дробного факторного эксперимента?
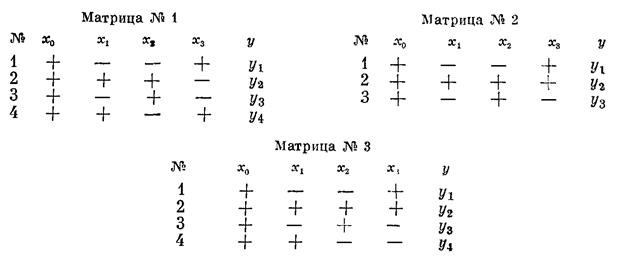
Рисунок 1.19 – Выбор матрицы планирования для дробного факторного эксперимента
Проверим свойства матрицы № 1. Каждый вектор-столбец матрицы, кроме первого, содержит равное число +1 и —1. Это означает, что выполняется условие: 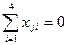 . Теперь перемножим каждую пару векторов-столбцов и посмотрим, будет ли сумма произведений равна 0. К сожалению,
. Теперь перемножим каждую пару векторов-столбцов и посмотрим, будет ли сумма произведений равна 0. К сожалению, 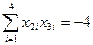 , т. е. совершена какая-то ошибка в выборе матрицы. Постараемся ее найти. Векторы-столбцы для х1 и х2 не вызывают сомнения. Ведь эта часть матрицы — полный факторный эксперимент
, т. е. совершена какая-то ошибка в выборе матрицы. Постараемся ее найти. Векторы-столбцы для х1 и х2 не вызывают сомнения. Ведь эта часть матрицы — полный факторный эксперимент 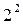 . А как построен вектор-столбец для х3? Элементы этого столбца имеют обратные знаки элементам соседнего столбца х2. Два этих столбца оказались взаимосвязанными: х3 = —х2. При этом
. А как построен вектор-столбец для х3? Элементы этого столбца имеют обратные знаки элементам соседнего столбца х2. Два этих столбца оказались взаимосвязанными: х3 = —х2. При этом 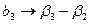 и
и 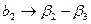 . В таком планировании не могут быть раздельно оценены основные эффекты. Значит, мы потеряли информацию о двух линейных коэффициентах нашей модели. Таким планированием воспользоваться невозможно.
. В таком планировании не могут быть раздельно оценены основные эффекты. Значит, мы потеряли информацию о двух линейных коэффициентах нашей модели. Таким планированием воспользоваться невозможно.
Матрица № 2 содержит всего три опыта. Три опыта недостаточны для оценки четырех коэффициентов: bо, b1, b2 и b3. Кроме того, ни одно из свойств, присущих полному факторному эксперименту, здесь не выполняется, за исключением нормировки.
Матрица № 3 сохраняет все свойства полного факторного эксперимента. Она дает возможность оценить свободный член bо и три коэффициента при линейных членах, потому что для х3 использован вектор-столбец х1х2 полного факторного эксперимента 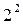 .
.
Если мы в дополнение к столбцам матрицы № 3 вычислим еще столбцы для произведений х1х3 и х2х3, то увидим, что элементы столбца х1х3 совпадут с элементами столбца x2, а элементы столбца х2х3 — с элементами столбца x1. Найденные нами коэффициенты будут оценками для совместных эффектов
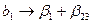 ;
; 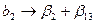 ;
; 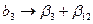 .
.
Такое планирование нас вполне устраивает. Мы смешали эффекты взаимодействия с основными эффектами. (Но все основные эффекты оцениваются раздельно друг от друга.) Так как постулируется линейная модель, то предполагается, что эффекты взаимодействия близки к нулю, и поэтому 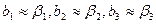 .
.
Мы рассмотрели самый простой случай: матрицу из четырех опытов для трехфакторного планирования. С увеличением числа факторов вопрос о минимизации числа опытов превращается в довольно сложную задачу. Рассмотрим ее детально. При этом нам не обойтись без новых определений и понятий.
Дробная реплика
Поставив четыре опыта для оценки влияния трех факторов, мы воспользовались половиной полного факторного эксперимента 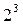 , или «полурепликой». Если бы мы х3 приравняли к —х1х2, то получили бы вторую половину матрицы
, или «полурепликой». Если бы мы х3 приравняли к —х1х2, то получили бы вторую половину матрицы 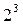 . В этом случае:
. В этом случае:
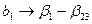 ;
; 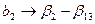 ;
; 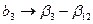 .
.
При реализации обеих полуреплик можно получить раздельные оценки для линейных эффектов и эффектов взаимодействия, как и в полном факторном эксперименте 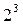 .
.
Объединение этих двух полуреплик и есть полный факторный4 эксперимент 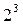 .
.
Матрица из восьми опытов для четырехфакторного планирования будет полурепликой от полного факторного эксперимента 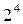 , а для пятифакторного планирования — четверть-репликой от
, а для пятифакторного планирования — четверть-репликой от 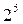 . В последнем случае два линейных эффекта приравниваются к эффектам взаимодействия. Для обозначения дробных реплик, в которых p линейных эффектов приравнены к эффектам взаимодействия, удобно пользоваться условным обозначением
. В последнем случае два линейных эффекта приравниваются к эффектам взаимодействия. Для обозначения дробных реплик, в которых p линейных эффектов приравнены к эффектам взаимодействия, удобно пользоваться условным обозначением 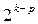 . Так, полуреплика от
. Так, полуреплика от 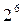 запишется в виде
запишется в виде 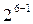 , а четверть-реплика от
, а четверть-реплика от 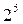 — в виде
— в виде 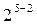 .
.
Условные обозначения дробных реплик приведены в таблице 1.12.
Таблица 1.12 – Условия обозначения дробных реплик и число опытов
| Число факторов | Дробная реплика | Условное обозначение | Число опытов | |
| Для ДФЭ | Для ПФЭ | |||
1/2-реплика от 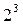
| 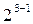
| |||
1/2-реплика от 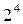
| 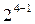
| |||
1/4-реплика от 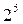
| 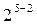
|
Продолжение таблицы 1.12
1/8-реплика от 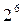
| 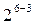
| |||
1/16-реплика от 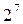
| 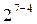
| |||
1/2-реплика от 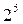
| 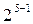
| |||
1/4-реплика от 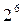
| 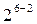
| |||
1/8-реплика от 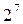
| 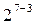
| |||
1/16-реплика от 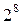
| 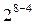
| |||
1/32-реплика от 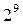
| 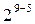
| |||
1/64-реплика от 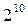
| 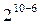
| |||
1/128-реплика от 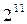
| 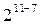
| |||
1/256-реплика от 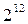
| 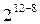
| |||
1/512-реплика от 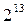
| 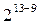
| |||
1/1024-реплика от 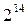
| 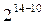
| |||
1/2028-реплика от 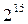
| 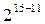
|
Дата добавления: 2021-11-16; просмотров: 649;











