Реплики большой дробности

Процедура выбора реплики любой дробности совершенно аналогична. При выборе 1/8-реплики 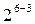можно воспользоваться вектор столбцами трех взаимодействий, например, так:

1) x4 = x1x2, x5 = x1x3, x6 = x2x3;

2) x4 = x1x3, x5 = x2x3, x6 = x1x2x3;

3) x4 = x1x2, x5 = x2x3 x6 = x1x2x3;

4) x4 = x1x2, x5 = x1x3 x6 = x1x2x3.

Для каждого из этих решений можно сделать шесть перестановок. Итого получается 24 возможности выбора 1/8-реплики. Это при условии, что мы всюду выбираем положительные генерирующие соотношения. Из четырех приведенных выше решений наименее удачно первое, поскольку все линейные эффекты смешиваются с парными взаимодействиями. Если априорно известно, что из всех взаимодействий наиболее существенно x1x2, то нужно выбрать второе решение, если x1x3 — третье, а если x2x3 — четвертое.

Мы последовательно рассмотрели реплики различной дробности: 1/2-реплику от 28, 1/2-реплику от 2*, 1/4-реплику от 25, 1/8-реплику от 2е и 1/16-реплику от 27. В первом случае необходимы четыре опыта. Во всех прочих случаях экспериментатор ставит восемь опытов. С ростом числа факторов увеличивается дробность реплик и усложняется система смешивания. Предельное число факторов для восьми опытов — семь. В этом случае оценивается восемь коэффициентов линейного уравнения 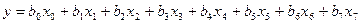, число степеней свободы равно нулю.

При числе факторов от 8 до 15 приходится ставить 16 опытов. С ростом числа факторов дробность реплик растет следующим образом: 1/32-реплика от 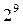, 1/64-реплика от 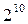, 1/128-реплика от 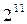, 1/256-реплика от 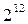, 1/512-реплика от 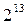, 1/1024-реплика от 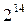и 1/2048-реплика от . Предельное число факторов для 16 опытов — пятнадцать. План с предельным числом факторов для данного числа опытов и заданной модели называется насыщенным. В этом случае число опытов равно числу оцениваемых коэффициентов. Все рекомендации для выбора системы смешивания аналогичны приведенным выше. Можно, далее, рассматривать построение дробных планов для числа факторов от 16 до 31 (при этом необходимо ставить 32 опыта), для числа факторов от 32 до 63 (здесь необходимы 64 опыта) и т. д. Однако для решения столь сложных задач рекомендуется применять методы отбора факторов, например метод случайного баланса [5].

Выводы. Дробные реплики находят широкое применение при получении линейных моделей. Целесообразность их применения возрастает с ростом количества факторов. В табл. 1.12 показано, что при исследовании влияния 15 факторов можно в 2048 раз сократить число опытов, применяя реплику большой дробности (16 опытов вместо 32768). Эффективность применения дробных реплик зависит от удачного выбора системы смешивания линейных эффектов с эффектами взаимодействия, а также от умелой стратегии экспериментирования в случае значимости некоторых взаимодействий. Априорные сведения о взаимодействиях могут оказать большую услугу экспериментатору.

При построении дробных реплик используют следующее правило: для того чтобы сократить число опытов при введении в планирование нового фактора, нужно поместить этот фактор в вектор-столбец матрицы, принадлежащий взаимодействию, которым можно пренебречь. Реплики, которые используются для сокращения опытов в 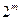раз, где m=1, 2, 3, 4, . . ., называются регулярными. Они пользуются большой популярностью, так как позволяют производить расчет коэффициентов уравнения так же просто, как и в случае полного факторного эксперимента.

При применении дробных реплик линейные эффекты смешиваются с эффектами взаимодействий. Чтобы определить систему смешивания, нужно знать определяющие контрасты и генерирующие соотношения. Определяющим контрастом называется символическое обозначение произведения любых столбцов, равное +1.

Чтобы определить, какие взаимодействия смешаны с данным линейным эффектом, нужно умножить определяющий контраст на этот линейный эффект и получить генерирующие соотношения. Например, если имеются следующие генерирующие соотношения: x1 = x2x3, x2 = x1x3 и x3 = x1x2, то определяющий контраст будет 1 = x1x2x3.

Эффективность реплики зависит от системы смешивания. Реплики, у которых линейные эффекты смешаны с взаимодействиями наивысшего порядка, являются наиболее эффективными, так как обладают наибольшей разрешающей способностью. Для освобождения линейных эффектов от взаимодействий первого порядка можно использовать метод «перевала». Смысл метода в добавлении новой реплики, все знаки которой противоположны исходной реплике. С ростом числа факторов быстро увеличивается число реплик различной дробности. Эти реплики характеризуются обобщающими определяющими контрастами, которые получаются перемножением по два, по три и т. д. исходных определяющих контрастов.