Будем рассматривать квадратичную форму (7) в евклидовом пространстве
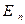 . Так как матрица
. Так как матрица 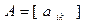
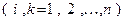 симметрична, то она может быть представлена
симметрична, то она может быть представлена
в виде:
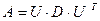
где – D диагональная матрица, на диагонали которой стоят собственные числа матрицы А, а U - ортогональная матрица, столбцами которой являются собственные вектора матрицы А. Как ранее отмечалось, что эти вектора в случае различных собственных чисел матрицы А являются линейно независимыми и образуют базис в 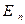 .
.
Столбцы матрицы U являются координатами некоторого ортонормированного базиса 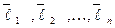 , в котором матрицa А имеет диагональный вид, и, следовательно, квадратичная форма – искомый канонический вид.
, в котором матрицa А имеет диагональный вид, и, следовательно, квадратичная форма – искомый канонический вид.
Соответствующее преобразование координат определяется соотношением:
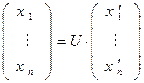 .
.
ПРИМЕР 2. Найти ортогональное преобразование, приводящее квадратичную форму
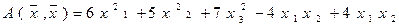 ,
,
заданную в евклидовом пространстве 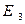 , к каноническому виду. Написать этот канонический вид.
, к каноническому виду. Написать этот канонический вид.
Матрица квадратичной формы имеет вид:
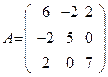 .
.
Определим собственные числа этой матрицы. Имеем:
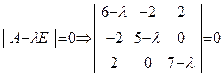 .
.
Раскрывая определитель, находим корни характеристического многочлена, которые являются собственными числами матрицы А. Итак, собственные числа этой матрицы суть 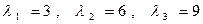 .
.
Соответствующие ортонормированные собственные векторы:
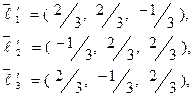
и, следовательно,
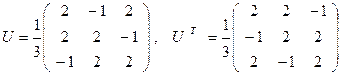 .
.
В базисе 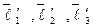 заданная квадратичная форма имеет вид:
заданная квадратичная форма имеет вид:
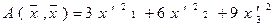 ,
,
а соответствующее преобразование координат:
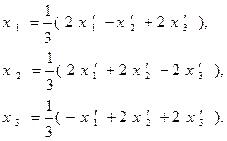 .
.
Дата добавления: 2016-06-05; просмотров: 1459;











