БИЛИНЕЙНЫЕ КВАДРАТИЧНЫЕ ФОРМЫ

4.1. Линейная функция

Рассмотрим простейшие числовые функции, аргументами которых являются вектора. Простейшей числовой функцией в пространстве L является линейная функция.

ОПРЕДЕЛЕНИЕ 1. Функция 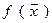называется линейной, если 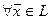ставит в соответствие число и при этом выполнены условия:

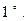
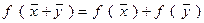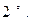
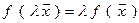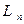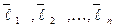Выберем в n-мерном линейном пространстве базис . Так как каждый вектор 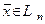можно представить в виде:

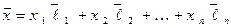то в силу свойства 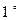линейной функции имеем:

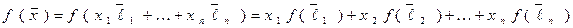Итак, в линейном n-мерном пространстве 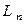с заданным базисом линейная функция может быть представлена в виде

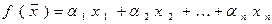, (1)

где 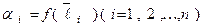постоянные, зависящие лишь от выбора базиса, а 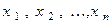- координаты вектора 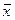в этом базисе.

Выясним, как меняются коэффициенты линейной функции при замене одного базиса другим.

Пусть 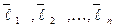и 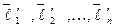- два базиса в 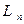. Предположим, что векторы 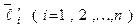выражаются через векторы базиса 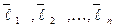следующим образом:

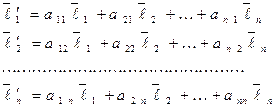В базисе 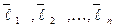линейная функция 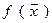определяется выражением

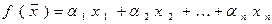, (2)

а в базисе 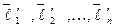- выражением

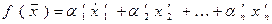. (3)

Так как

то

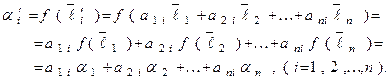
Следовательно, коэффициенты линейной формы преобразуются при переходе к другому базису так же, как векторы базиса этого пространства.

4.2. Билинейные формы

ОПРЕДЕЛЕНИЕ 2. Выражение 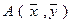называется билинейной функцией (билинейной формой) от векторов 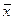и 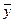, если:

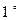. При фиксированном 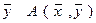есть линейная функция от 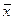, то есть:

а) ,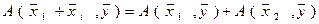

б) .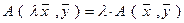

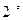. При фиксированном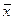 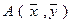есть линейная функция от 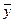, то есть:

а) ,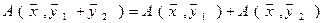

б) .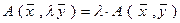

ОПРЕДЕЛЕНИЕ 3. Билинейная функция (форма) называется симметричной, если для всех векторов 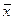и 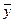имеет место равенство:

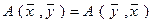(4)

В частности, из определения скалярного произведения 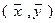в евклидовом пространстве Е следует, что это произведение является симметричной билинейной формой.

4.3. Матрицы билинейной формы

Выберем в n-мерном пространстве 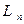какой-либо базис 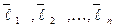и выразим билинейную форму 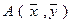через коэффициенты 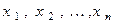и 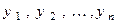векторов 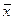и 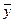в этом базисе. Имеем:

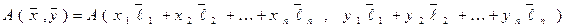
В силу свойств а) и б) пункта 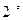билинейной формы, имеем:

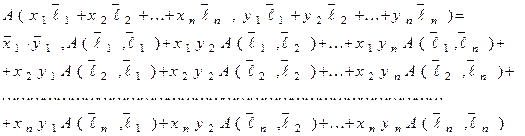
Или, короче:

.

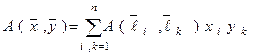Обозначим постоянные 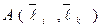через 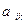. Тогда в заданном базисе 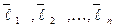всякая билинейная форма в n-мерном пространстве может быть записана в виде:

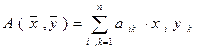. (5)

ОПРЕДЕЛЕНИЕ 4. Матрицу 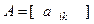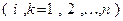, составленную из коэффициентов 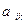многочлена (5), называют матрицей билинейной формы 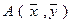в базисе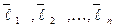

Таким образом, в каждом базисе пространства 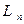билинейная форма 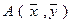определяется своей матрицей:

.

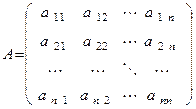4.4. Преобразование матрицы билинейной формы

<2 3 456 7 8 >

Дата добавления: 2016-06-05; просмотров: 1518;