К каноническому виду

а) Метод Лагранжа выделения полных квадратов.

Пусть квадратичная форма 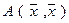имеет в базисе 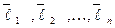вид (7). Для приведения формы 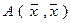к сумме квадратов методом Лагранжа рассмотрим случай квадратичной формы, у которой все коэффициенты 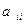(при квадратах 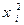), 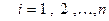равны нулю и в то же время эта квадратичная форма не равна тождественно нулю, то есть в ней есть отличное от нуля хотя бы одной произведение, например, .

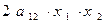Выполним преобразование базиса, при котором коэффициенты векторов в старом и новом базисах связаны формулами:

.

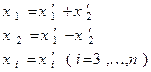Тогда:

.

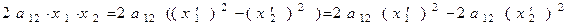Таким образом, всегда найдется такой базис, в котором в записи (7) хотя бы один коэффициент при квадрате 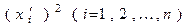.отличен от нуля.

В дальнейшем будем считать, что 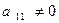. (Если 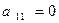, то отличен от нуля коэффициент при квадрате какой-нибудь другой координаты и к рассматриваемому случаю можно прийти, иначе, занумеровав векторы 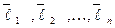, что также является некоторым преобразованием базиса).

Рассмотрим часть квадратичной формы, содержащей 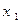, то есть

.

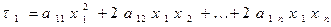Дополним эту сумму до полного квадрата:

,

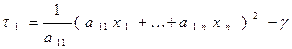где 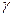есть алгебраическая сумма членов, не зависящих от 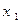. Если теперь сделать замену

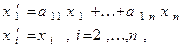
то квадратичная форма в новом базисе примет вид

.

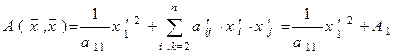В полученной форме выделено слагаемое 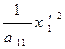, а оставшаяся часть А, является квадратичной формой в .

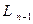Далее эти рассуждения повторяются для исходной квадратичной формы 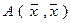и т.д. Конечным результатом является то, что она приводится к нормальной форме.

ПРИМЕР 1. Методом Лагранжа привести к каноническому виду квадратичную форму

.

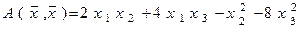Первое преобразование:

.

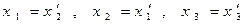Тогда получим:

.

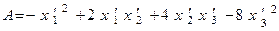Второе преобразование:

.

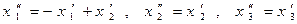Получим новое выражение для квадратичной формы:

.

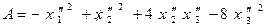Третье преобразование:

.

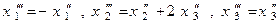форма примет канонический вид:

.

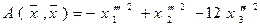При этом

.

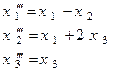б) Метод собственных векторов.