Формулы преобразования координат при изменении базиса
Пусть 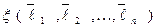 и
и 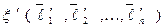 два различных базиса в
два различных базиса в 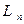 . Каждый из векторов базиса
. Каждый из векторов базиса 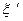 разложим по базису
разложим по базису 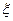 следующим образом:
следующим образом:
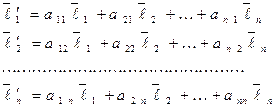 . (13)
. (13)
ОПРЕДЕЛЕНИЕ 7. Матрицей перехода 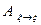 от базиса
от базиса 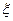 к базису
к базису 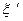 называется матрица вида:
называется матрица вида:
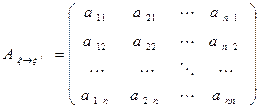 ,
,
в которой i-й столбец есть коэффициенты i-го уравнения системы (13).
Далее обозначим через 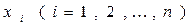 коэффициенты вектора
коэффициенты вектора 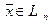 в первом базисе
в первом базисе 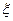 , а через
, а через 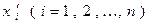 его координаты во втором базисе
его координаты во втором базисе 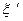 . Пусть требуется найти связь координат
. Пусть требуется найти связь координат 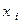 через
через 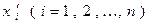 .
.
Имеем:
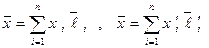
или
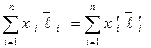 . (14)
. (14)
Подставим в правую часть выражения (14) вместо 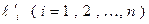 их выражения (13). Получим:
их выражения (13). Получим:
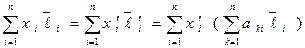 (15)
(15)
или
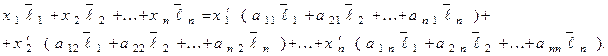
Так как, система векторов 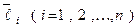 линейно независима, то координаты при них в правой и левой частях равенства должны быть равны.
линейно независима, то координаты при них в правой и левой частях равенства должны быть равны.
Имеем
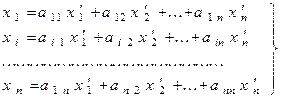 ,
,
или
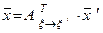 (16)
(16)
где
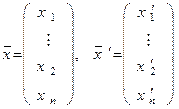 .
.
Таким образом, координаты 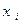
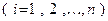 вектора
вектора 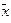 в базисе
в базисе 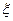 выражаются через координаты
выражаются через координаты 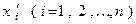 того же вектора
того же вектора 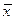 во втором базисе
во втором базисе 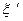 с помощью матрицы
с помощью матрицы 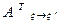 , то есть матрицы, транспонированной к
, то есть матрицы, транспонированной к 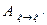 .
.
Поскольку матрица 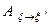 является невырожденной, то из формулы (16) можно получить:
является невырожденной, то из формулы (16) можно получить:
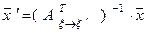 (17)
(17)
где координаты 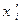 вектора
вектора 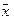 во втором базисе
во втором базисе 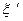 выражаются через координаты
выражаются через координаты 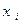 в первом базисе с помощью матрицы
в первом базисе с помощью матрицы 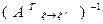 , являющейся обратной к
, являющейся обратной к 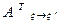 .
.
ПРИМЕР. Найти координаты вектора 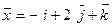 в базисе
в базисе 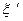 , состоящем из векторов
, состоящем из векторов 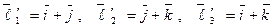 .
.
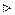 Решение. В соответствие с формулой (13) имеем:
Решение. В соответствие с формулой (13) имеем:
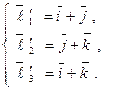
Запишем матрицы перехода 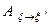 и
и 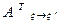 .
.
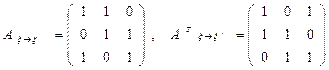 .
.
Обращая матрицу 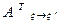 . и используя формулу (17), находим
. и используя формулу (17), находим
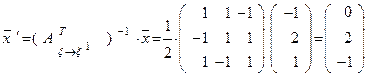
То есть
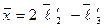 .
.
Откуда координаты вектора 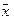 в базисе
в базисе 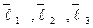 принимают значения
принимают значения
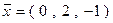 .
. 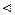
2. ЛИНЕЙНОЕ Пространство со скалярным
Дата добавления: 2016-06-05; просмотров: 1919;











