Неравенство Коши-Буняковского
ОПРЕДЕЛЕНИЕ 2. Длиной вектора 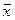 в евклидовом пространстве называетсячисло равное:
в евклидовом пространстве называетсячисло равное:
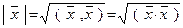 (2)
(2)
ОПРЕДЕЛЕНИЕ 3. Углом между векторами 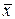 и
и 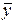 мы назовем число, определенное выражением:
мы назовем число, определенное выражением:
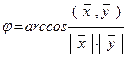 , (3)
, (3)
или
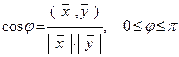 . (4)
. (4)
ОПРЕДЕЛЕНИЕ4. Векторы 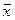 и
и 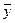 называютсяортогональными,еслиугол между ними равен
называютсяортогональными,еслиугол между ними равен 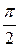 .
.
В этом случае из формулы (1) следует:
( 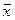 ,
, 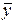 )=0. (5)
)=0. (5)
Н е р а в е н с т в о К о ш и- Б у н я к о в с к о г о. Так как косинус угла между двумя векторами определяется выражением (4)
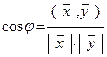 , (6)
, (6)
то
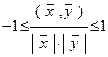 .
.
Откуда
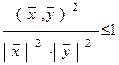 .
.
или
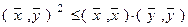 . (7)
. (7)
Неравенство (7) называется неравенством Коши-Буняковского.
Если скалярное произведение задается формулой
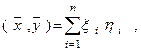
причем
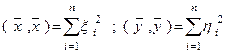 ,
,
то неравенство (7) примет вид
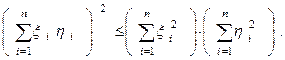
Т е о р е м а. 3. Для любых векторов 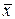 и
и 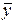 в евклидовом пространстве Е имеет место неравенство:
в евклидовом пространстве Е имеет место неравенство:
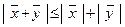 . (8)
. (8)
Д о к а з а т е л ь с т в о.
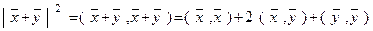 .
.
Так как 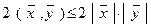 , то
, то
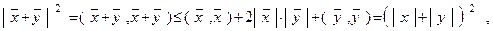
то есть
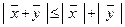 ,
,
что и требовалось доказать.
2.2. Ортогональный и орто-нормированный
базисы в пространстве Е
В линейном пространстве у нас нет оснований предпочесть одни базисы другим. Там все базисы равноправны. В евклидовом пространстве существуют наиболее удобные базисы, а именно, ортогональные базисы. Они играют здесь ту же роль, что и прямоугольные системы координат в аналитической геометрии.
ОПРЕДЕЛЕНИЕ 5. Будем говорить, что n векторов 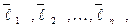 ни один из которых не равен нулю, образуют ортогональный базисв n-мерном евклидовомпространстве
ни один из которых не равен нулю, образуют ортогональный базисв n-мерном евклидовомпространстве 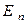 , если они попарно ортогональны, то есть:
, если они попарно ортогональны, то есть:
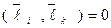 при
при 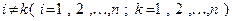 .
.
ОПРЕДЕЛЕНИЕ 6. Векторы 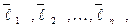 ни один из которых не равен нулю, образуют ортогональный нормированный базис, если они попарно ортогональны и имеют каждый длину равную единице, то есть, если выполняется равенство:
ни один из которых не равен нулю, образуют ортогональный нормированный базис, если они попарно ортогональны и имеют каждый длину равную единице, то есть, если выполняется равенство:
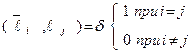 (9)
(9)
Для того, чтобы данное нами определение ортогонального и ортонормированных базисов было корректным, необходимо доказать, что входящие в определение векторы 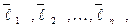 действительно образуют базис, то есть являются линейно независимыми.
действительно образуют базис, то есть являются линейно независимыми.
Докажем, что равенство
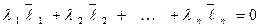 (10)
(10)
возможно лишь, если 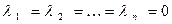 , то есть является тривиальным. Умножим обе части равенства (10) скалярно на
, то есть является тривиальным. Умножим обе части равенства (10) скалярно на 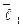 . Получим:
. Получим:
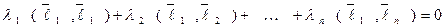 .
.
Но по определению ортогонального базиса
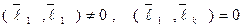 при
при 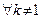 .
.
Следовательно, 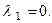 Аналогично, умножая (10) на
Аналогично, умножая (10) на 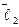 , получим l2=0 и т. д. Таким образом, соотношение (10) выполнено, если
, получим l2=0 и т. д. Таким образом, соотношение (10) выполнено, если 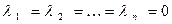 , то есть векторы
, то есть векторы 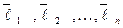 являются независимы, что и доказывает корректность утверждения.
являются независимы, что и доказывает корректность утверждения.
Чтобы доказать существование ортогональных базисов в евклидовом пространстве 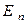 , воспользуемся, так называемым, процессом ортогонализации.
, воспользуемся, так называемым, процессом ортогонализации.
2.3. Ортогонализация базиса в пространстве 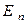
Процесс ортогонализации состоит в том, что из не ортогональных, но линейно независимых векторов 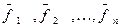 , можно построить систему попарно ортогональных векторов
, можно построить систему попарно ортогональных векторов 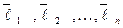 . Опишем процесс их построения. Пусть даны n линейно независимых векторов
. Опишем процесс их построения. Пусть даны n линейно независимых векторов 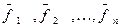 . По этим векторам построим n попарно ортогональных векторов
. По этим векторам построим n попарно ортогональных векторов 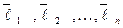 . Сначала положим
. Сначала положим 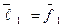 . Вектор
. Вектор 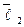 будем искать в виде:
будем искать в виде: 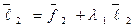 , где число l1 подберем таким образом, чтобы выполнялось условие
, где число l1 подберем таким образом, чтобы выполнялось условие 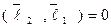 .
.
Имеем:
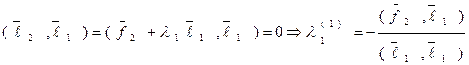 (11)
(11)
Предположим, что построена система попарно ортогональных и отличных от нуля векторов 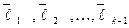 . Далее вектор
. Далее вектор 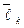 будем определять так:
будем определять так:

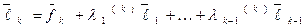 , (12)
, (12)
то есть вектор 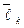 мы получаем из вектора
мы получаем из вектора 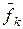 путем "исправления" его с помощью линейной комбинации уже построенных векторов
путем "исправления" его с помощью линейной комбинации уже построенных векторов 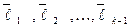 .
.
Коэффициенты 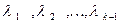 находим из условия ортогональности вектора
находим из условия ортогональности вектора 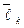
 к векторам
к векторам 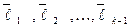 . Последовательно умножим соотношение (12) на
. Последовательно умножим соотношение (12) на 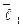 , затем на
, затем на 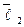 и т.д. Имеем
и т.д. Имеем

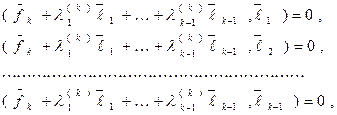 ( 13)
( 13)
Так как векторы 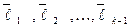 попарно ортогональны, то равенства (13) запишутся так:
попарно ортогональны, то равенства (13) запишутся так:

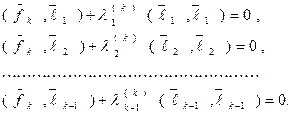
Отсюда находим:
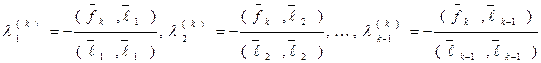 (14)
(14)
До сих пор не было использовано то, что векторы 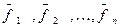 линейно независимы. Это будем использовать при доказательстве того, что построенный вектор
линейно независимы. Это будем использовать при доказательстве того, что построенный вектор 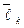 отличен от нуля. Заметим предварительно, что вектор
отличен от нуля. Заметим предварительно, что вектор 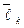 есть линейная комбинация векторов
есть линейная комбинация векторов 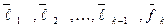 . Но, с другой стороны, вектор
. Но, с другой стороны, вектор 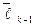 можно заменить линейной комбинацией
можно заменить линейной комбинацией 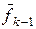 и векторов
и векторов 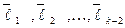 . В итоге, вектор
. В итоге, вектор 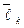 записывается в виде:
записывается в виде:

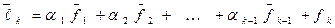 . (15)
. (15)
Теперь ясно, что 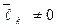 .Так как, в противном случае, правая часть равенства (15) была бы нулем, что противоречит линейной независимости векторов
.Так как, в противном случае, правая часть равенства (15) была бы нулем, что противоречит линейной независимости векторов 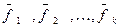 .
.
Итак, доказано, что 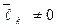 .
.
Мы построили по векторам 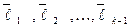 и
и 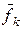 вектор
вектор 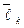 . Таким же образом по
. Таким же образом по 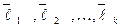 и
и 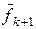 мы построим
мы построим 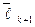 и т.д.
и т.д.
Продолжая этот процесс до тех пор, пока не будут исчерпаны заданные векторы 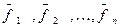 . Получаем n отличных от нуля и попарно ортогональных векторов
. Получаем n отличных от нуля и попарно ортогональных векторов 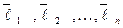 , которые образуют ортогональный базис в исходном евклидовом пространстве
, которые образуют ортогональный базис в исходном евклидовом пространстве 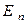 .
.
Т е о р е м а 4. Во всяком n-мерном евклидовом пространстве 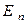 существует ортогональный базис.
существует ортогональный базис.
Д о к а з а т е л ь с т в о. По определению n-мерного пространства 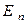 в нем существует базис линейно независимых векторов
в нем существует базис линейно независимых векторов 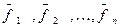 . С помощью процесса ортогонализации из векторов
. С помощью процесса ортогонализации из векторов 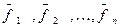 можно построить ортогональный базис
можно построить ортогональный базис 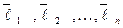 , что и доказывает теорему.
, что и доказывает теорему.
2.4. Скалярное произведение векторов в евклидовом пространстве
Пусть 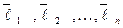 - ортогональный базис евклидова пространства Е. Найдем, как выражается скалярное произведение двух векторов через их координаты в этом базисе.
- ортогональный базис евклидова пространства Е. Найдем, как выражается скалярное произведение двух векторов через их координаты в этом базисе.
Пусть 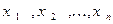 - координаты вектора
- координаты вектора 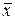 , а
, а 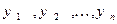 - координаты вектора
- координаты вектора 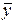 в этом базисе, то есть:
в этом базисе, то есть:
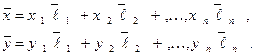
Тогда:
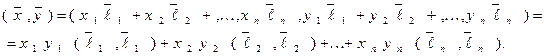 (16)
(16)
Если базис 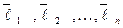 является ортонормированным, то есть
является ортонормированным, то есть
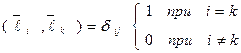 , (17)
, (17)
то выражение (16) в таком базисе примет вид
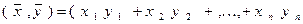 ). (18)
). (18)
Таким образом, в нормированном ортогональном базисе скалярное произведение двух векторов равно сумме произведений их соответствующих координат.
2.5. Изоморфизм евклидовых пространств
Если рассмотреть ряд n-мерных евклидовых пространств, то эти пространства могут отличаться одно от другого во всяком случае способом задания векторов базиса. Возникает вопрос: какие из этих пространств действительно различны и какие различия являются лишь чисто внешними?
Для того, чтобы вопрос был точно поставлен, нужно определить, какие два
евклидова пространства будем считать несущественно различающимися (изоморфными).
ОПРЕДЕЛЕНИЕ 7. Два евклидовых пространства 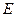 и
и 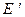 называются изоморфными, если между их элементами можно установить взаимно однозначное соответствие
называются изоморфными, если между их элементами можно установить взаимно однозначное соответствие 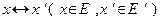 так, что:
так, что:
1 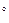 . Если
. Если 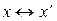 и
и 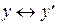 , то
, то 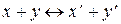 .
.
2  . Если
. Если 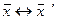 , то
, то 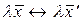 .
.
3 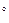 . Если
. Если 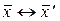 и
и 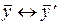 , то
, то 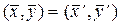 .
.
Таким образом, два евклидовых пространства 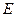 и
и 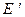 изоморфны, если они изоморфны как линейные пространства. И этот изоморфизм таков, что он сохраняет скалярное произведение соответствующих векторов.
изоморфны, если они изоморфны как линейные пространства. И этот изоморфизм таков, что он сохраняет скалярное произведение соответствующих векторов.
Дата добавления: 2016-06-05; просмотров: 2133;











