При изменении базиса
Пусть даны в n-мерном линейном пространстве 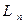 два базиса:
два базиса: 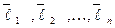 и
и 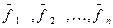 . Причем, векторы второго базиса
. Причем, векторы второго базиса 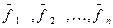 выражаются через векторы базиса
выражаются через векторы базиса 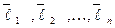 формулами:
формулами:
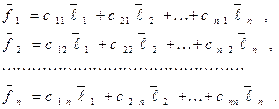
Матрицу
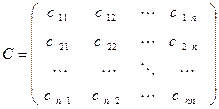
назовем матрицей перехода от базиса 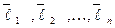 к базису
к базису 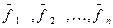 .
.
Пусть 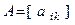
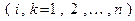 есть матрица билинейной формы
есть матрица билинейной формы 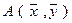 в базисе
в базисе 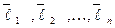 , а
, а 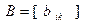 матрица той же билинейной формы в базисе
матрица той же билинейной формы в базисе 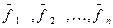 . Наша задача состоит в том, чтобы по матрице
. Наша задача состоит в том, чтобы по матрице 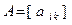
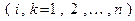 найти матрицу
найти матрицу 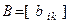
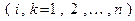 .
.
По определению 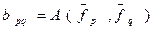 , то есть
, то есть 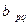 - значение билинейной формы
- значение билинейной формы 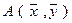 при
при 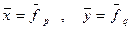 .
.
Для того, чтобы найти это значение, то есть 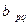 , воспользуемся формулой (5), подставив в нее вместо
, воспользуемся формулой (5), подставив в нее вместо 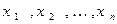 и
и 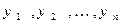 координаты векторов
координаты векторов 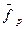 и
и 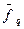 в базисе
в базисе 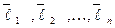 , то есть числа
, то есть числа 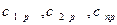 и
и 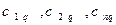 . Получим:
. Получим:
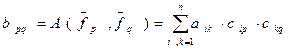 . (6)
. (6)
Это и есть искомая формула.
Запишем ее в матричной форме. Для этого положим 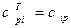 . Таким образом,
. Таким образом, 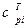 является элементами матрицы
является элементами матрицы 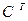 , транспонированной к матрице С. С учетом этого выражение (6) можно записать так:
, транспонированной к матрице С. С учетом этого выражение (6) можно записать так:
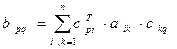
или
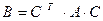 .
.
Итак, если А и В суть матрицы билинейной формы 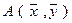 соответственно в базисах
соответственно в базисах 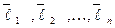 и
и 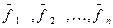 ., то преобразование матрицы билинейной формы при переходе от одного базиса к другому будет иметь вид:
., то преобразование матрицы билинейной формы при переходе от одного базиса к другому будет иметь вид:
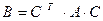
где С - матрица перехода от базиса 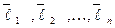 к базису
к базису 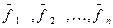 ., а
., а 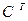 - транспонированная матрица.
- транспонированная матрица.
4.5. Квадратичные формы
Пусть - 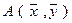 симметричная билинейная форма.
симметричная билинейная форма.
ОПРЕДЕЛЕНИЕ 1. Функция 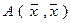 , которая получается из билинейной формы
, которая получается из билинейной формы 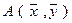 , если положить в ней
, если положить в ней 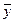 =
= 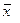 , называется квадратичнойформой.
, называется квадратичнойформой.
Всякая квадратичная форма 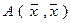 , в базисе
, в базисе 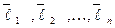 евклидового пространства Еn выражается следующей формулой:
евклидового пространства Еn выражается следующей формулой:
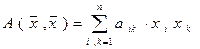 , (7)
, (7)
где 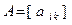
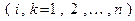 симметричная матрица
симметричная матрица 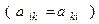 квадратичной формы и
квадратичной формы и 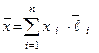 .
.
В некотором базисе выражение (7) квадратичной формы может не содержать произведений 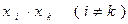 , то есть
, то есть
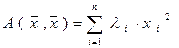 , (8)
, (8)
Выражение (8) называется каноническим видом квадратичной формы. В частности, если 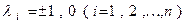 , то получаем нормальный видквадратичной формы
, то получаем нормальный видквадратичной формы 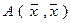 .
.
Для всякой квадратичной формы существует такой базис, в котором она имеет канонический вид.
4.6. Методы приведения квадратичной формы
Дата добавления: 2016-06-05; просмотров: 1543;











