Определение базиса и размерность пространства L
Пусть 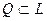 - произвольное множество векторов линейного пространства.
- произвольное множество векторов линейного пространства.
ОПРЕДЕЛЕНИЕ 4. Упорядоченная система векторов 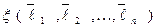
называется базисом в Q, если:
a) 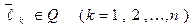 ;
;
б) система векторов 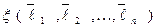 линейно независимая;
линейно независимая;
в) для 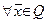 найдутся такие числа
найдутся такие числа 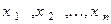 , что
, что
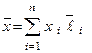 . (6)
. (6)
Формула (6) называется разложением вектора 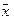 по базису Q , а коэффициенты
по базису Q , а коэффициенты 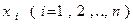 – координатами этого вектора в базисе Q.
– координатами этого вектора в базисе Q.
Если 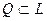 обладает базисом, то говорят, что линейное пространство L имеет ранг Q (ranq Q).
обладает базисом, то говорят, что линейное пространство L имеет ранг Q (ranq Q).
ОПРЕДЕЛЕНИЕ 5. Линейное пространство L называется n-мерным, если в нем существует n линейно независимых векторов и обозначается так 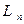 . В противном случае, пространство L называется бесконечно мерным.
. В противном случае, пространство L называется бесконечно мерным.
Т е о р е м а 2. Каждый вектор 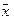 из
из 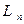 можно представить, и притом единственным образом, как линейную комбинацию векторов базиса.
можно представить, и притом единственным образом, как линейную комбинацию векторов базиса.
Д о к а з а т е л ь с т в о. Пусть векторы 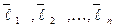 образуют базис в
образуют базис в 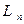 . Присоединим к ним произвольный вектор
. Присоединим к ним произвольный вектор 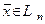 . Система векторов состоит уже из
. Система векторов состоит уже из 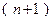 -го вектора
-го вектора 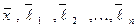 . Поэтому по определению n-мерного пространства они должны быть линейно зависимыми, то есть
. Поэтому по определению n-мерного пространства они должны быть линейно зависимыми, то есть
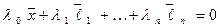 , (7)
, (7)
причем
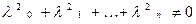 .
.
Число 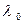 заведомо отлично от нуля, так как иначе из формулы (7) следовала бы линейная зависимость векторов
заведомо отлично от нуля, так как иначе из формулы (7) следовала бы линейная зависимость векторов 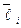 . Выразим из (7) вектор
. Выразим из (7) вектор 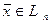 .
.
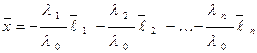 . (7)
. (7)
Таким образом, мы доказали, что каждый вектор 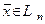 есть линейная комбинация векторов базиса
есть линейная комбинация векторов базиса 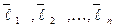 . Докажем, что вектор
. Докажем, что вектор 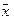 разлагается единственным образом по базису
разлагается единственным образом по базису 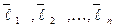 .
.
Доказательство проведем от противного.
Пусть существует два разложения
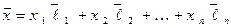 (8)
(8)
и
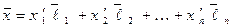 . (9)
. (9)
Вычитая из (8) разложение (9), получим:
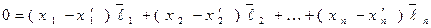 . (10)
. (10)
Так как вектора базиса 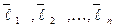 .линейно независимые, то (10) возможно лишь, если:
.линейно независимые, то (10) возможно лишь, если:
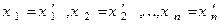 .
.
Что и требовалось доказать.
3.3. Изоморфизм n-мерных линейных пространств
ОПРЕДЕЛЕНИЕ 6. Два линейных пространства и называются изоморфными, если между векторами 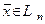 и
и 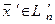 можно установить взаимно однозначное соответствие
можно установить взаимно однозначное соответствие 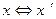 так, что если вектору
так, что если вектору 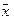 соответствует вектор
соответствует вектор 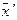 , а вектору
, а вектору 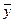 соответствует вектор
соответствует вектор 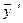 и выполнены условия:
и выполнены условия:
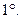 Вектору
Вектору 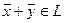 соответствует
соответствует 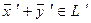 . (11)
. (11)
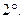 Вектору
Вектору 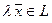 соответствует
соответствует 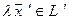 . (12)
. (12)
Из определения изоморфизма следует, что если 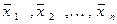 из
из 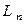 . а векторы
. а векторы 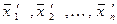 - из
- из 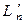 , то
, то
в соответствии с равенствами (11) - (12) получаем, что линейно независимым векторам из 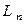 соответствуют линейно независимые векторы из
соответствуют линейно независимые векторы из 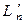 и обратно.
и обратно.
Заметим, что два линейных пространства различной размерности не изоморфны друг другу.
Дата добавления: 2016-06-05; просмотров: 1935;











