ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА ЛИНЕЙНЫЕ.

Дифференциальное уравнение первого порядка называется линейным, если оно имеет вид

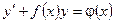(1)

где 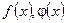- некоторые (непрерывные) функции переменной 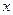. В случае, когда функция 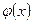тождественно равна нулю, уравнение называется однородным, в противном случае – неоднородным.

Рассмотрим один из возможных способов решения уравнения (1).

Идея метода Бернулли состоит в отыскании решения линейного дифференциального уравнения первого порядка в виде произведения двух неизвестных дифференцируемых функци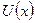й и .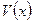

Так как

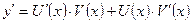
то из (1) следует

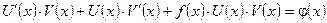(2)

Вынесем за скобки во втором и третьем слагаемых :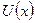

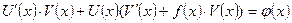(3)

Поскольку равнение одно, а неизвестных функций две, то одну из них можно выбрать произвольно. Выберем ее таким образом, чтобы обратился в нуль коэффициент при .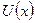

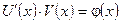
получаем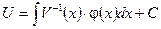

Таким образом, решение исходного уравнения (1) сводится к решению двух уравнений с разделяющимися переменными.

Пример.

Найти общее решение дифференциального уравнения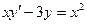

Решение.

Приводим уравнение к каноническому виду, разделив на 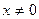, и тем самым устанавливаем тип этого уравнения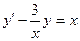

Решим уравнение, используя подстановку Бернулли.

Подставляя, получаем 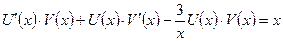, группируя первое и третье слагаемые, выносим за скобки :

: ;

:

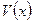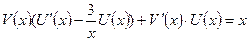
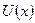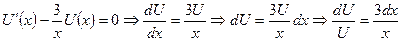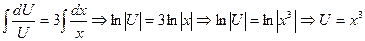
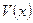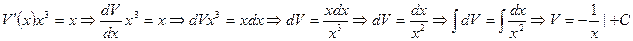
Тогда общее решение запишется в виде

.

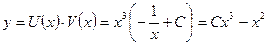КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Какое уравнение называется дифференциальным уравнением с разделяющимися переменными?

2. Какое уравнение называется однородным дифференциальным уравнением первого порядка?

3. Какое уравнение называется линейным дифференциальным уравнением первого порядка?

4. Какое уравнение называется уравнением с разделяющимися переменными?