Теорема (достаточный признак расходимости числового ряда).

Если предел общего члена числового ряда (1) при 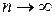равен не нулю, т.е.

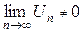, (2)

то соответствующий ряд расходится.

Пример. Проверить выполнение необходимого признака сходимости для числового ряда .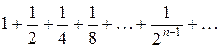

Решение.По условиюn-й член числового ряда равен 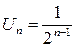. Находим предел n-го члена этого ряда: 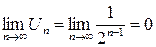. Следовательно, необходимое условие сходимости ряда выполняется.

Пример.Проверить выполнение необходимого признака сходимости для числового ряда .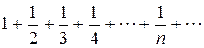

Решение. Это гармонический ряд. Находим предел n-ого члена ряда 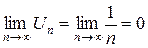. необходимое условие сходимости ряда выполняется.

Замечание. Выполнение необходимого признака сходимости числового ряда, т.е. 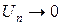, не является достаточным, для утверждения, что числовой ряд сходится. Ряд может быть как сходящимся, так и расходящимся.

Пример. Исследовать сходимость ряда .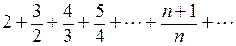

Решение. Общий член данного числового ряда равен 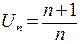. Тогда предел n-го члена ряда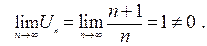

Следовательно, данный числовой ряд расходится, так как не выполняется необходимый признак сходимости числового ряда.

Пример. Исследовать сходимость ряда: .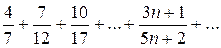

Решение.По условию общий член числового ряда равен 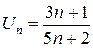, тогда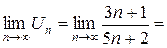

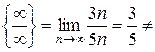
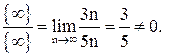
Исследуемый ряд расходится, так как не выполняется необходимый признак сходимости числового ряда.