А) Граничные условия первого рода

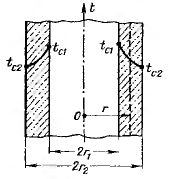
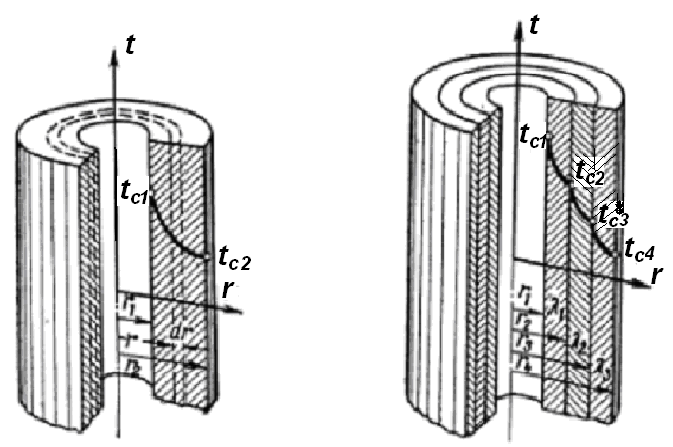
Рассмотрим стационарный процесс теплопроводности в цилиндрической стенке (трубе) с внутренним диаметром d₁=2r и наружным диаметром d₂=2r₂ (рис. 2.6).
На поверхностях стенки заданы постоянные температуры t_c1 и t_c2
В заданном интервале температур коэффициент теплопроводности материала стенки l является постоянной величиной. Необходимо найти распределение температур в цилиндрической стенке и тепловой поток через нее.
В рассматриваемом случае дифференциальное уравнение теплопроводности удобно записать в цилиндрической системе координат: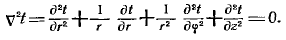
При этом ось Oz совмещена с осью трубы.
При заданных условиях температура изменяется только в радиальном направлении, и температурное поле будет одномерным. Поэтому

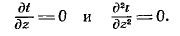
б) Граничные условия третьего рода (теплопередача)

Рассмотрим однородную цилиндрическую стенку (трубу) с постоянным коэффициентом теплопроводности l. Заданы постоянные температуры подвижных сред t_ж1 и t_ж2 и постоянные значения коэффициентов теплоотдачи на внутренней и наружной поверхностях трубы a₁ и a₂ (рис. 2.7)

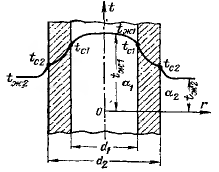
Необходимо найти q_l и t_c. Будем полагать, что длина трубы велика по сравнению с толщиной стенки. Тогда потерями теплоты с торцов трубы можно пренебречь, и при установившемся тепловом режиме количество теплоты, которое будет передаваться от горячей среды к поверхности стенки, проходить через стенку и отдаваться от стенки к холодной жидкости, будет одно и то же.

Следовательно, можно написать:

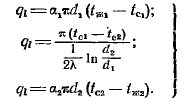
Складывая уравненияполучаем температурный напор:

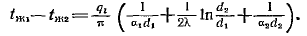
Отсюда следует:

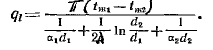
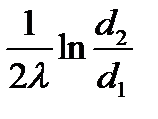Величина R_l = 1/k_l, обратная линейному коэффициенту теплопередачи, называется линейным термическим сопротивлением теплопередачи. Она равна

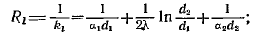
здесь R_l измеряется в м×К/Вт.
Отдельные составляющие полного термического сопротивления представляют собой:
1/a₁d₁ и 1//a₂d₂ —термические сопротивления теплоотдачи на соответствующих поверхностях, обозначим их соответственно R_l1 и R_l2; - термическое сопротивление

теплопроводности стенки, обозначим его через R_lc.
Следует отметить, что линейные термические сопротивления теплоотдачи для трубы определяются не только коэффициентами теплоотдачи a₁ и a₂, но и соответствующими диаметрами

КРИТИЧЕСКИЙ ДИАМЕТР ЦИЛИНДРИЧЕСКОЙ СТЕНКИ
Рассмотрим влияние изменения наружного диаметра на термическое сопротивление однородной цилиндрической стенки. Из (2-51) имеем:

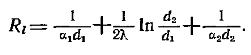
При постоянных значениях a₁, d₁, l и a₂ полное термическое сопротивление теплопередачи цилиндрической стенки будет зависеть от внешнего диаметра. Из уравнения (2-51) следует, что при этих условиях 1/a₁d₁ º R_lc =const.
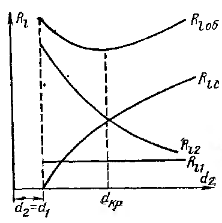
Термическое сопротивление теплопроводности c увеличением d₂ будет возрастать, а термическое сопротивление теплоотдачи 1/a₂d₂ = R_l2 будет уменьшаться. Очевидно, что полное термическое сопротивление будет определяться характером изменения составляющих R_lc и R_l2.Изменение частных термических со противлении изображено на рис. 2-8.

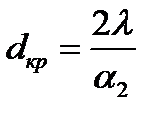
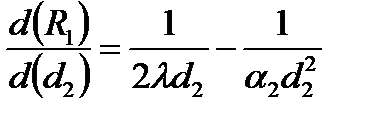Для того чтобы выяснить, как будет изменяться R_l при изменении толщины цилиндрической стенки, исследуем R_l как функцию d₂. Возьмем производную от R_l по d₂ и приравняем нулю:

Значение d₂ из последнего выражения соответствует экстремальной точке кривой R_l =f(d₂). Значение внешнего диаметра трубы, соответствующе-го минимальному полному термическому сопротивлению теплопередачи, называется критическим диаметром и обозначается d_кр. Рассчитывается он по формуле При d₂ < d_кр с увеличением d₂ полное термическое сопротивление теплопередачи снижается, так как увеличение наружной поверхности оказывает на термическое сопротивление большее влияние, чем увеличение толщины стенки.
При d₂ > d_кр сувеличением d₂ термическое сопротивление теплопередачвозрастает, что указывает на доминирующее влияние толщины

8.Передача теплоты через шаровую стенку.

а) Граничные условия первого рода
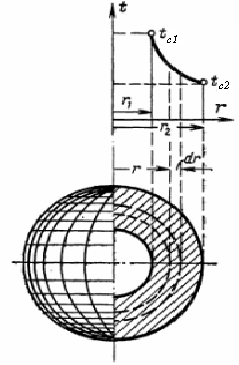
Пусть имеется полый шар с радиусами r₁и r₂, постоянным коэффициентом теплопроводности lи с заданными равномерно распределенными температурами поверхностей t_c1и t_c2. Так как в рассматриваемом случае температура измеряется только в направлении радиуса шара, то дифференциальное уравнение теплопроводности в сферических координатах принимает вид: 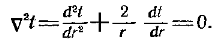(1)
Граничные условия запишутся:
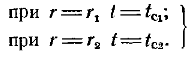(2)
После первого интегрирования уравнения (1) получаем: 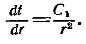Второе интегрирование дает: 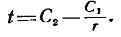(3)
Постоянные интегрирования в уравнении (3) определяются из граничных условий (2). При этом получим:

С₁= - (t_c1-t_c2)/(1/r₁ – 1/r₂);

С₂=t_c1–((t_c1-t_c2)/(1/r₁ – 1/r₂))*1/r₁
Подставляя значения С₁и С₂в уравнение (3), получаем выражения для температурного поля в шаровой стенке:
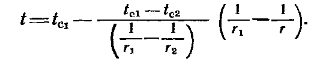(4)
Для нахождения количества теплоты, проходящей через шаровую поверхность величиной Fв единицу времени, можно воспользоваться законом Фурье:
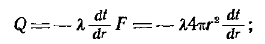здесь Qизмеряется в ваттах.
Если в это выражение подставить значение градиента температуры dt/dr, то получим:

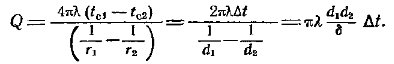
Эти уравнения являются расчетными формулами теплопроводности шаровой стенки. Из уравнения (2.64) следует, что при постоянномlтемпература в шаровой стенке меняется по закону гиперболы.