Предельный признак сравнения числовых рядов.

Если для числовых рядов (1), (2) отношение их общих членов 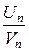стремится к некоторому положительному и конечному пределу при 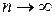, т.е.

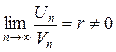, (3)

то данные числовые ряды сходятся и расходятся одновременно.

Пример. Исследовать сходимость числового ряда .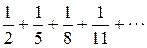

Решение.Определяем n-й член ряда. Знаменатели членов числового ряда образуют арифметическую прогрессию с общим членом 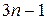, поэтому 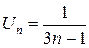. Сравним данный числовой ряд с гармоническим рядом, общий член которого равен 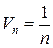. Найдем предел отношения общих членов данного и гармонического числовых рядов (1.3.3): .

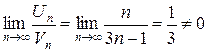Следовательно, по предельному признаку сравнения рядов, данный числовой ряд расходится.

Признак Даламбера.

Если для числового знакоположительного ряда (1) существует предел отношения последующего члена к предыдущему при 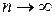, т.е.

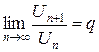, (4)

то при q < 1 ряд (1) сходится, при q > 1 ряд (1) расходится.

Замечание.Если q = 1, тогда следует применить другой достаточный признак сходимости.

Замечание.Признак Даламбера рекомендуется использовать, если общий член числового ряда содержит показательные и (или) факториальные элементы относительно n.

Пример. Исследовать сходимость ряда: .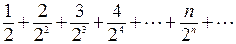

Решение. В соответствии с рекомендациями замечания 1.3.2, применим достаточный признак сходимости Даламбера. По условию 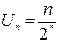; 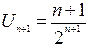. По формуле (4) находим .

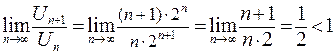Следовательно, по признаку Даламбера данный числовой ряд сходится.

Замечание.Чтобы от члена U_n числового ряда перейти к (n+1)-му члену, нужно в формуле для U_n заменить n на n+1.

Пример. Исследовать сходимость ряда .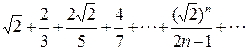

Решение.Используем достаточный признак сходимости Даламбера. Имеем 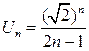, тогда 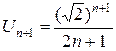.По формуле (4) находим

.

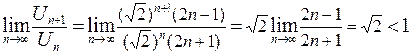Значит, по признаку сходимости Даламбера данный числовой ряд расходится.

Пример. Исследовать сходимость ряда .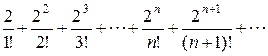

Решение.применяем достаточный признак сходимости Даламбера. Имеем

.

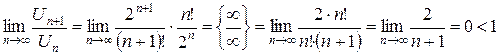Следовательно, по признаку сходимости Даламбера данный числовой ряд сходится.