Алгебраические и трансцендентные уравнения

 

Рассмотрим уравнение f(x) = 0, где функция f(x) оп­ределена и непрерывна в некотором конечном или беско­нечном интервале а < х < b.

Определение 2.1. Корнем уравнения f(x) = 0 называет­ся значение ξ, обращающее функцию f(x) в нуль, т. е. та­кое, что f(ξ) = 0.

Определение 2.2. Уравнение f(x) = 0 называется алгеб­раическим, если функция f(x) является многочленом f(x) = Рn(х) = апхп + ап-1хn-1 + ... + а1х + а0, в противном случае уравнение f(x) = 0 называется трансцендентным.

Встречающиеся на практике уравнения часто не уда­ется решить аналитическими методами. Для решения таких уравнений используются численные методы.

Алгоритм нахождения корня уравнения с помощью численного метода состоит из двух этапов:

1) отделение или локализация корня, т. е. установле­ние промежутка [а, b], в котором содержится один ко­рень;

2) уточнение значения корня методом последователь­ных приближений.

 

2.1. Методы локализации корней

 

1.Аналитический метод

Теоретической основой алгоритма отделения корней служит теорема

Коши о промежуточных значениях не­прерывной функции.

Теорема 2.1. Если функция f(x) непрерывна на отрез­ке [a, b] u f(a) = A, f(b) = В, то для любой точки С, лежа­щей между А и В, существует точка c Î [а, b], что f(c) = C.

Следствие. Если функция f(x) непрерывна на отрезке [a,b] и на его концах принимает значения разных зна­ков, то на этом отрезке существует, хотя бы один ко­рень уравнения f(x) = 0.

Пусть область определения и непрерывности функции является конечным отрезком [a,b]. Разделим отрезок на n частей:

ak = а + kh, k = 0, 1, ... п, h = (b - а)/п.

Вычисляя последовательно значения функции в точ­ках а0, а1, ..., ап, находим такие отрезки [ak, ak + 1], для которых выполняется условие

f(ak)×f(ak + 1) < 0, (2.1)

т. е. f(ak) < 0, f(ak + 1) > 0 или f(ak) > 0, f(ak + 1) < 0. Эти отрезки и содержат хотя бы по одному корню.

Теорема 2.2. Если непрерывная функция f(x) монотон­на на отрезке [а, b] на его концах принимает значения разных знаков, то на этом отрезке существует един­ственный корень уравнения f(x) = 0.

Если функция f(х) дифференцируема и ее производная сохраняет знак на отрезке [а, b], то f(х) монотонна на этом отрезке.

Если производная f '(х) легко вычисляется и нетрудно определить ее корни, то для отделения корней уравнения f(х) = 0 можно применить следующий алгоритм:

1) найти критические точки, в которых производная f '(х) равна нулю или не существует, и определить ин­тервалы знакопостоянства производной f '(х) (на этих интер­валах функция f (х) может иметь только по одному корню);

2) составить таблицу знаков функции f (х), приравни­вая переменную х к критическим и граничным значени­ям, или близким к ним;

3) определить отрезки, на концах которых функция принимает значения разных знаков.

 

2. Графический метод

 

Для отделения корней уравнения естественно приме­нять графический метод. График функции у = f (х) с уче­том свойств функции дает много информации для опре­деления числа корней уравнения f (х) = 0.

До настоящего времени графический метод предлага­лось применять для нахождения грубого значения корня или интервала, содержащего корень, затем применять итерационные методы, т. е. методы последовательных приближений для уточнения значения корня. С появле­нием математических пакетов и электронных таблиц ста­ло возможным вычислять таблицы значений функции с любым шагом и строить графики с высокой точностью.

Это позволяет уточнять очередной знак в приближенном значении корня при помощи следующего алгоритма:

1) если функция f(x) на концах отрезка [а,b] значения разных принимает значения разных знаков то делим отрезок на 10 равных частей и находим ту часть, которая содержит корень (таким способом мы можем уменьшить длину отрезка, содержащего корень, в 10 раз);

2) повторим действия предыдущего пункта для полу­ченного отрезка.

Этот процесс можно продолжать до тех пор, пока длина отрезка не станет меньше заданной погрешности.

2.2. Методы уточнения корней

 

После того как найден интервал, содержащий корень, применяют итерационные методы уточнения корня с за­данной точностью.

1. Метод половинного деления

 

Метод половинного деления (метод бисекций, метод дихотомии) для решения уравнения f(x) = 0 заключает­ся в следующем.

Пусть известно, что функция непрерыв­на и принимает на концах отрезка [а, b] значения разных знаков, тогда корень содержится в интервале (а, b). Раз­делим интервал на две половины и дальше будем рассмат­ривать ту половину, на концах которой функция прини­мает значения разных знаков (рис. 1). Этот новый отрезок [x1, b] снова делим на два равных отрезка и выби­раем из них тот, который содержит корень (отрезок [х1 х2] на рис. 1). Этот процесс продолжается до тех пор, пока длина очередного отрезка не станет меньше тре­буемой величины погрешности. На рис. 1 середина от­резка

[х1, х2] совпадает с точкой пересечения графика с осью абсцисс, т. е. точка х3 «попадает» в корень уравне­ния, и в этом случае процесс деления заканчивается.

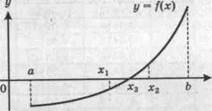
Рис. 1. Метод половинного деления

 

Более строгое изложение алгоритма метода половинного деления:

1) вычислим х = (a + b)/2; f(x);

2) если f(x) = 0, переходим к п. 5;

3) если f(x) × f(a) < 0, то b = х, иначе, а = х;

4) если |b - а| > ε, переходим к п. 1;

5) выводим значение х;

6) конец.

2. Метод итераций

 

Метод простых итераций для уравнения f(x) = 0 заключается в следующем:

1) Исходное уравнение преобразуют к виду, удобному для итераций:

x = φ(х). (2.2)

2) Выбирают начальное приближение х0 и вычисляют последующие приближения по итерационной формуле
xk = φ(хk-1), k =1,2, ... (2.3)

Если существует предел итерационной последовательности, 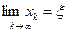, он является корнем уравнения f(x) = 0, т. е. f(ξ) =0.

 

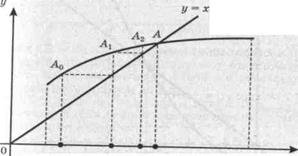
y = φ(х)

 

 

a x0 x1 x2 ξ b

 

Рис. 2. Сходящийся процесс итераций

 

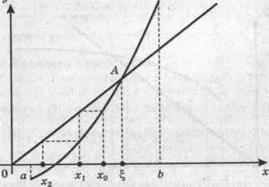
На рис. 2 показан процесс получения очередного приближения по методу итераций. Последовательность приближений сходится к корню ξ.

Теоретические основы для применения метода итера­ций дает следующая теорема.

Теорема 2.3. Пусть выполняются условия:

1) корень уравнения х = φ(х) принадлежит отрезку [а, b];

2) все значения функции φ(х) принадлежат отрезку [а, b],т. е. а ≤ φ(х)≤ b;

3) существует такое положительное число q < 1, что производная φ'(x) во всех точках отрезка [а, b] удовлет­воряет неравенству |φ'(x) | ≤ q.

Тогда:

1) итерационная последовательность хп = φ(хп-1)(п = 1, 2, 3, ...) сходится при любом x0Î [а, b];

2) предел итерационной последовательности является корнем уравнения

х = φ(x), т. е. если 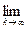xk = ξ, то ξ= φ(ξ);

3) справедливо неравенство, характеризующее ско­рость сходимости итерационной последовательности

|ξ-xk| ≤ (b-a)×qk. (2.4)

 

Очевидно что, эта теорема ставит, довольно, жесткие условия, которые необходимо проверить перед примене­нием метода итераций. Если производная функции φ(x) по модулю больше единицы, то процесс итераций расхо­дится (рис. 3).

y = φ(x) y = x

 

Рис. 3. Расходящийся процесс итераций

 

В качестве условия сходимости итерационных методов чисто используется неравенство

|xk - xk-1| ≤ ε. (2.5)

3. Метод хорд

Метод хорд заключается в замене кривой у = f(x) отрезком прямой, проходящей через точки (а, f(a)) и (b, f(b)) рис. 4). Абсцисса точки пересечения прямой с осью ОХ принимается за очередное приближение.

Чтобы получить расчетную формулу метода хорд, за­пишем уравнение прямой, проходящей через точки (a, f(a)) и (b, f(b)) и, приравнивая у к нулю, найдем х:

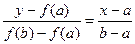Þ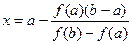

Алгоритм метода хорд:

 

1) пусть k = 0;

2) вычислим следующий номер итерации: k = k + 1.

Найдем очередное k-e приближение по формуле:

xk = a - f(a)(b - a)/(f(b) - f(a)).

Вычислим f(xk);

3) если f(xk)= 0 (корень найден), то переходим к п. 5.

Если f(xk) ×f(b)>0, то b = xk, иначе a = xk;

4) если |xk – xk-1| > ε, то переходим к п. 2;

5) выводим значение корня xk;

6) конец.

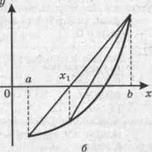
Замечание. Действия третьего пункта аналогичны действи­ям метода половинного деления. Однако в методе хорд на каж­дом шаге может сдвигаться один и тот же конец отрезка (пра­вый или левый), если график функции в окрестности корня выпуклый вверх (рис. 4, а) или вогнутый вниз (рис. 4, б).Поэтому в критерии сходимости используется разность сосед­них приближений.

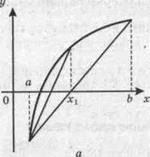
Рис. 4. Метод хорд

4. Метод Ньютона (касательных)

Пусть найдено приближенное значение корня уравнения f(x)= 0, и обозначим его хп.Расчетная формула метода Ньютона для определения очередного приближения xn+1 может быть получена двумя способами.

Первый способ выражает геометрический смысл метода Ньютона и состоит в том, что вместо точки пересечения графика функции у = f(x)с осью Оx ищем точку пересечения с осью Оx касательной, проведенной к графику функции в точке (xn, f(xn)),как показано на рис. 5. уравнение касательной имеет вид у - f(xn)= f '(xn)(x - xn).

 

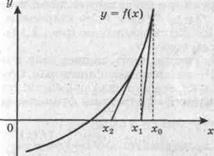
Рис. 5. Метод Ньютона (касательных)

В точке пересечения касательной с осью Оx переменная у = 0. Приравнивая у к нулю, выразим х и получим формулу метода касательных:

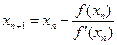(2.6)

Второй способ: разложим функцию f(x)в ряд Тейлора в окрестности точки х = хn:

Ограничимся линейными слагаемыми относительно (х - хп),приравняем к нулю f(x) и, выразив из получен­ного уравнения неизвестное х,обозначив его через хn+1получим формулу (2.6).

Приведем достаточные условия сходимости метода Ньютона.

Теорема 2.4. Пусть на отрезке [а, b]выполняются ус­ловия:

1) функция f(x)и ее производные f '(х)и f ''(x)непре­рывны;

2) производные f '(x)и f ''(x)отличны от нуля и сохра­няют определенные постоянные знаки;

3) f(a)× f(b) < 0 (функция f(x)меняет знак на отрезке).
Тогда существует отрезок [α, β], содержащий искомый корень уравнения f(x) = 0, на котором итерационная пос­ледовательность (2.6) сходится. Если в качестве нулевого приближения х0выбрать ту граничную точку [α, β], в ко­торой знак функции совпадает со знаком второй произ­водной,

т.е. f(x0)× f"(x0)>0, то итерационная последо­вательность сходится монотонно

Замечание. Отметим, что метод хорд как раз идет с противо­положной стороны, и оба этих метода могут друг друга допол­нять. Возможен и комбинированный метод хорд-касательных.

5. Метод секущих

Метод секущих может быть получен из метода Ньютона при замене производной приближенным выражени­ем – разностной формулой:

, ,

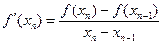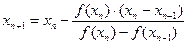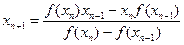. (2.7)

В формуле (2.7) используются два предыдущих при­ближения хп и xn-1.Поэтому при заданном начальном приближении х0необходимо вычислить следующее приближение x1, например, методом Ньютона с приближенной заменой производной по формуле

,

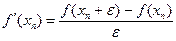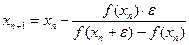
Алгоритм метода секущих:

 

1) заданы начальное значение х0и погрешность ε. Вычислим

;

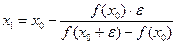2) для п = 1, 2, ... пока выполняется условие |xn – xn-1| > ε, вычисляем хп+1 по формуле (2.7).

2.3.Системы нелинейных уравнений

Система п нелинейных уравнений с п неизвестными Имеет вид

fk(x1, х2, ... , хп) = 0,1 ≤ k ≤ n. (2.8)

1.Графический метод.

Систему двух нелинейных уравнений можно решить приближенно

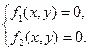(2.9)

графическим способом. Для этого достаточно преобразовать систему к виду

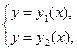(2.10)

 
 

построить графики функций у = y1(x), у = у2(х)и найти координаты точек пересечения графиков (рис. 6).

При использовании электронных таблиц или математических пакетов решение можно уточнить графически, сужая отрезок [a, b] около корня xs.

Для уточнения решения (xs, ys)можно также приме­нить метод итераций или Ньютона.

2. Метод итераций

Приведем систему (2.8) к виду, удобному для итераций:

xk = φk(x1, x2,..., xn), 1 ≤ k ≤ n (2.11)

Выберем начальное приближение к корню ( ), последующие приближения вычислим по формулам

,

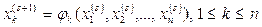s = 0, 1, 2, … (2.12)

Приведем без доказательства достаточные условия сходимости метода итераций. Обозначим точное решение системы (2.8) .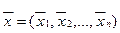

Определение 2.3. Назовем ε-окрестностью точки 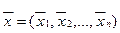множество точек х = (х1, х2, ... , хп),удовлетворяющих условиям

.

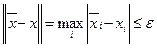Теорема 2.5. Пусть в некоторой ε-окрестности точного решения 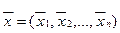частные производные 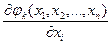существуют и удовлетворяют одному из трех неравенств

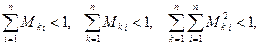(2.13)

 

где (максимум берется по всем точкам ε-окрестности).

Если начальное приближение х0 = ( 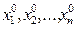) принадлежит ε-окрестности точного решения, то метод простой итерации (2.12) сходится к точному решению.

3. Метод Ньютона

Строгие формулировки теорем об условиях сходимос­ти метода Ньютона достаточно громоздки, на практике часто ограничиваются следующим рассуждением.

Пусть для системы нелинейных уравнений

fk(х1, х2, ... , хn) = 0, 1 ≤ k ≤ п,

в некоторой ε-окрестности точного решения не равен пулю определитель матрицы частных производных (мат­рицы Якоби):

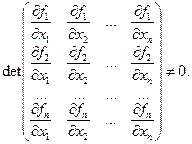
Тогда существует начальное приближение х0 =( 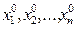), принадлежащее ε-окрестности точ­ного решения (достаточно близкое к точному решению), что метод Ньютона сходится к точному решению.

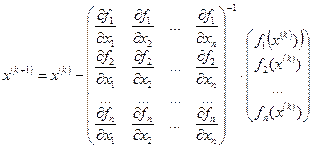, (2.14)

k = 0,1, ...

Для системы двух уравнений метод Ньютона (2.14) имеет вид:

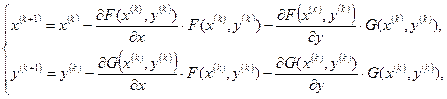(2.15)

k = 0, 1, ...

<== предыдущая лекция | следующая лекция ==>
Математическая модель и погрешности | Вычислительные методы линейной алгебры

Дата добавления: 2020-08-31; просмотров: 1141;

Поиск по сайту:

Воспользовавшись поиском можно найти нужную информацию на сайте.

Поделитесь с друзьями:

Считаете данную информацию полезной, тогда расскажите друзьям в соц. сетях.
Poznayka.org - Познайка.Орг - 2016-2024 год. Материал предоставляется для ознакомительных и учебных целей.
Генерация страницы за: 0.038 сек.