А. Уравнения движения точки в декартовых координатах

Действительно, если заданы уравнения движения точки в декартовой системе координат

,

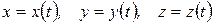то проекции силы на оси координат определяются из уравнений (1.2)

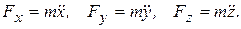(1.3)

Зная проекции силы на координатные оси, легко определить модуль силы и направляющие косинусы углов силы с осями координат.

Пример 1. Груз спускается вниз по шероховатой наклонной плоскости, расположенной под углом a к горизонту, двигаясь согласно уравнению 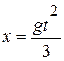. Определить модуль силы трения скольжения груза о плоскость.

Решение. Совместим ось x c направлением движения тела. К грузу приложены три силы: сила трения 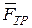, реакция поверхности 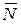и вес тела 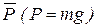(рис.1.1). Составим дифференциальное уравнение движения груза в проекции на ось х:

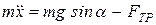. (а)

Так как 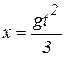, то 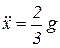, уравнение (а) примет вид

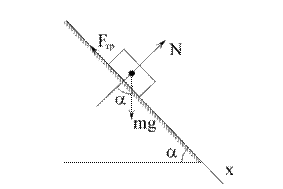Рис. 1.1

,

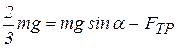откуда

.

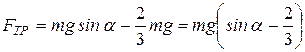Следует отметить, что решение накладывает ограничения на условия задачи и справедливо только, когда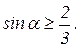

Пример 2. Материальная точка массы m движется согласно уравнениям 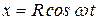, 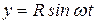. Определить силу 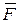, вызывающую это движение, если известно, что сила зависит только от положения точки, т.е. .

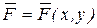Решение. Уравнение траектории движения, согласно заданным уравнениям движения: 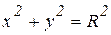, т. е. точка вращается по окружности против хода часовой стрелки (рис. 1.2). Совместим систему координат с центром окружности и составим уравнение (1.3) в проекциях на оси получим:

.

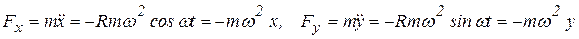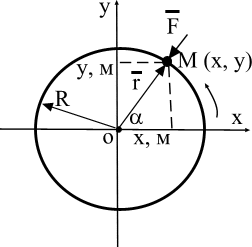Рис. 1.2

Модуль силы

,

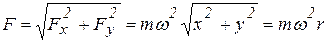где r – модуль радиус-вектора материальной точки 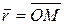(рис. 1.2).

Направление силы 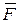определяем по направляющим косинусам:

.

.

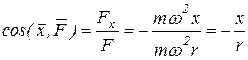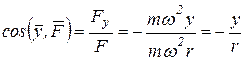Так как величины 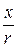и 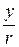определяют также углы, образуемые соответственно осями х и у с радиус-вектором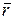 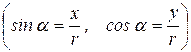, то сила 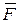направлена от точке М к центру окружности (рис. 1.2). Такая сила называется центральной.