Алгоритм исчисления порядка

Вход: g – порождающий элемент циклической группы порядка n, a 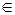G, с≈10 – параметр надежности.

Ш.1. Выбирается факторная база S={p₁, p₂,…,p_t}. (Если G=Z_p^*, то S состоит из t первых простых чисел.)

Ш.2. Выбрать случайное k: 0≤k<n и вычислить g^k.

Ш.3. Попытаться разложить g^k по факторной базе:

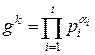, α_i≥0.

Если это не удалось, вернуться на Шаг 2.

Ш.4. Логарифмируя обе части получившегося выражения, получаем

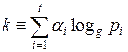(mod n) *

В этом выражении неизвестными являются логарифмы.

Это сравнение с t неизвестными следует запомнить.

Ш.5. Если сравнений вида (*), полученных на Шаге 4, меньше, чем t+c, то вернуться на Шаг 2.

Ш.6. Решить систему t+c сравнений с t неизвестными вида (*), составленную на Шагах 2-5.

Ш.7. Выбрать случайное k: 0≤k<n и вычислить ag^k.

Ш.8. Попытаться разложить ag^k по факторной базе:

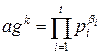, β_i≥0.

Если это не удалось, вернуться на Шаг 7.

Ш.9. Логарифмируя обе части последнего равенства, получаем

x= ,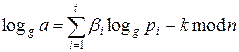

где log_gp_i (1≤i≤t) вычислены на Шаге 6 как решение системы сравнений.

Выход. x = log_ga mod n.

В том случае, когда G=Z_p^*, в качестве факторной базы S берут t первых простых чисел. Такой выбор оправдан следующим наблюдением. Число, наугад выбранное из множества целых чисел, с вероятностью 1/2 делится на 2, с вероятностью 1/3 – на 3, с вероятностью 1/5 – на 5 и т.д. Поэтому можно ожидать, что в промежутке от 1 до p—1 найдется достаточно много чисел, в разложении которых участвуют только маленькие простые делители из множества S. Именно такие числа отыскиваются на шагах 2 и 7.

Параметр c вводится для того, чтобы система сравнений, решаемая на Шаге 6, имела единственное решение. Дело в том, что полученная система может содержать линейно зависимые сравнения. Считается, что при значении с порядка 10 и большом p система сравнений имеет единственное решение с высокой вероятностью.

Пример.

G=Z^*₇₁, g=7, a=17, n=φ(71)=70.

S={2, 3, 5, 7} (Шаг 1). (Можем сразу указать log₇7 mod 70=1).

Теперь будем перебирать k для составления системы сравнений вида * (Шаги 2—5).

k=2, 7² mod 71=49=7·7. (поскольку log₇7 уже вычислен, это сравнение нам не пригодится).

k=3, 7³ mod 71=59.

k=4, 7⁴ mod 71=58=2·29.

k=5, 7⁵ mod 71=51=3·17.

k=6, 7⁶ mod 71=2 6≡log₇2(mod 70)

k=7, 7⁷ mod 71=14=2·7 7≡log₇2+log₇7(mod 70)

k=8, 7⁸ mod 71=27=3³ 8≡3log₇3(mod 70)

k=9, 7⁹ mod 71=47.

k=10, 7¹⁰ mod 71=45=3²·5 10≡2log₇3+log₇5(mod 70)

Теперь имеем достаточно сравнений для того, чтобы определить логарифмы от элементов факторной базы. Вот эти сравнения:

6≡log₇2(mod 70)

7≡log₇2+log₇7(mod 70)

8≡3log₇3(mod 70)

10≡2log₇3+log₇5(mod 70)

Решая полученную систему, получаем (Шаг 6):

log₇2≡6(mod 70), log₇3≡26(mod 70),

log₇5≡28(mod 70), log₇7≡1(mod 70).

Перейдем к Шагам 7—9:

k=1, 26·7 mod 71=40=2³·5 log₇26≡3log₇2+log₇5—1(mod 70)

log₇26≡3·6+28—1(mod 70)

log₇26≡45(mod 70)

Проверка: 7⁴⁵ mod 71 = 26. Верно.

Ответ: log₇26≡45(mod 70).

Замечание: Для случая G=Z_p и для случая G=F₂m составляет L_q[1/2,c], где q есть мощность G, с > 0 – константа. Алгоритм, имеющий наилучшую оценку сложности (по времени) для дискретного логарифмирования в Z_p есть вариант алгоритма исчисления индексов под названием «метод решета числового поля» (number field sieve), для дискретного логарифмирования в F₂m - вариант данного алгоритма под названием «алгоритм Копперсмита» (Coppersmith’s algorithm). Эти алгоритмы слишком сложны, чтобы приводить их здесь.