ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА ОДНОРОДНЫЕ

Дифференциальное уравнение вида

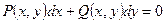(1)

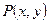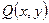называется однородным уравнением первого порядка, если функции и являются однородными функциями одного измерения. Функция 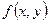называется однородной функцией своих аргументов измерения 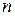, если

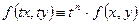(2)

Например, функция 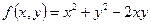является однородной функцией аргументов 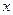и 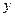измерения два, так как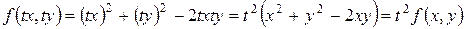

При 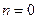имеем однородную функцию нулевого измерения. Например,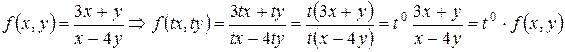

Решение однородных дифференциальных уравнений первого порядка (1) сводится к решению уравнений с разделяющимися переменными путем замены 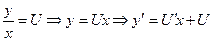вычислив интеграл и сделав обратную замену 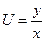получим общий интеграл уравнения (1).

Пример.

Найти общее решение дифференциального уравнения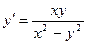

Решение.Убедимся в том, что уравнение является однородным.

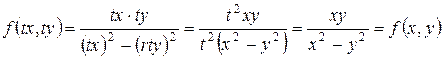
Функция 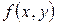- однородная, нулевого измерения, следовательно, данное уравнение является однородным дифференциальным уравнением.

Заменив в исходном уравнении 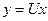, 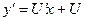получим уравнение 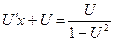или .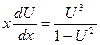

Это уравнение с разделяющимися переменными. Разделив их, получим 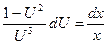, разделив почленно числитель на знаменатель правой части равенства, имеем 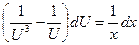. Проинтегрировав последнее уравнение, найдем 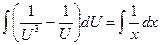. 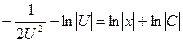, или, упростив, получим , .

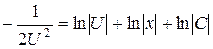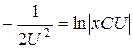Подставив в полученное равенство 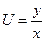, общее решение исходного уравнения запишется в виде 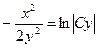, а после преобразования: .

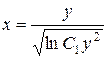Пример.Решить уравнение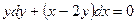

Решение.

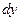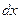Это однородное дифференциальное уравнение первого порядка, так как коэффициенты при и являются однородными функциями первого порядка. Разделим уравнение относительно 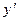, полагая 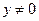, получаем .

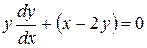Разделим обе части равенства на :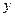

.

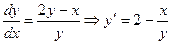Сделаем замену: .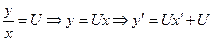

Тогда имеем ; ; .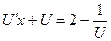

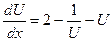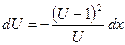Это уравнение с разделяющимися переменными, разделим их , , , , .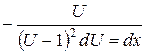

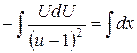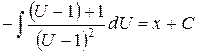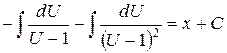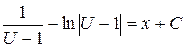Так как 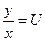, то 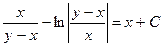- общий интеграл уравнения.

Потерянным при преобразовании является решение 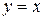, которое является особым.

Уравнения, которые при помощи определенной замены переменных приводятся к однородным, называют уравнениями, сводящимися к однородным. К таким уравнениям относятся, например, уравнения вида

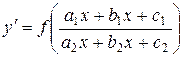
где 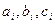- заданные постоянные 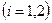. Замена

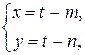
где 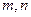- решения системы уравнений

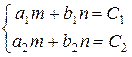
сводит решение уравнения к решению однородного уравнения:

.

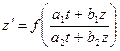Решив последнее уравнение и сделав обратную замену

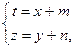
получим общий интеграл исходного уравнения.