ПОНЯТИЕ ЧИСЛОВОГО РЯДА. СУММА ЧИСЛОВОГО РЯДА. СВОЙСТВА СХОДЯЩИХСЯ РЯДОВ.
Если U1, U2, U3,…, Un… некоторая бесконечная последовательность действительных чисел, то выражение
U1 + U2 + U3 + …+ Un +…(1)
называют бесконечным числовым рядом или просто числовым рядом.
Числовой ряд (1) можно записать в свернутом виде 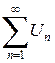 .
.
числа U1, U2, U3,…, Un … называются членами ряда, а Un называется общим членом ряда. Зависимость Un от номера n является законом образования членов ряда. Обычно полагают n равным 1, 2, 3,…, а иногда ряд начинают с n = 0.
Пример.Записать первых пять членов числового ряда 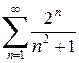 .
.
Решение.Общий член данного ряда равен 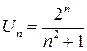 . Тогда при
. Тогда при 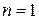 имеем
имеем 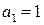 ; при
; при 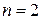 получим
получим 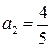 . Аналогично находим
. Аналогично находим 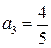 ;
; 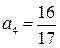 ;
; 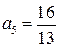 .
.
Пример.Найтиобщий член ряда: 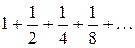 .
.
Решение.Сопоставляя номер члена ряда и его величину, получим
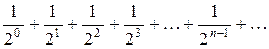 .
.
Таким образом, общий член ряда равен 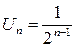 .
.
Следует заметить, что члены данного ряда образуют бесконечную геометрическую прогрессию, причем 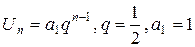 .
.
Числовой ряд вида (1.1.2)
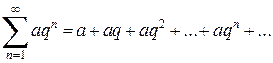 , (2)
, (2)
где q – знаменатель геометрической прогрессии, которую образуют члены данного ряда, называется рядом геометрической прогрессии.
Числовой ряд вида (3)
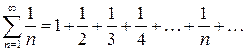 (3)
(3)
называется гармоническим рядом.
Числовой ряд вида (1.1.4)
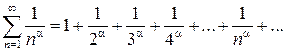 (4)
(4)
называется обобщенным гармоническим рядом.
Пример. Найтиобщий член ряда 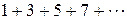 .
.
Решение.Сопоставляя номер члена ряда и его величину, получим
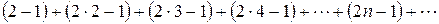 .
.
Таким образом, общий член ряда равен 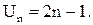
Следует заметить, что члены рассматриваемого числового ряда образуют арифметическую прогрессию, причем 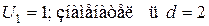 .
.
Пример. Найтиобщий член ряда 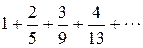 .
.
Решение.Сопоставляя номер члена этого числового ряда и его величину, получим
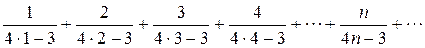 .
.
Таким образом, общий член рассматриваемого ряда равен 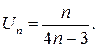
Дата добавления: 2021-09-25; просмотров: 479;











