Признак сравнения числовых рядов.

Пусть даны положительные числовые ряды

U₁+ U₂+U₃+…+U_n+…,(1)

V₁+ V₂+V₃+…+V_n+….(2)

Если числовой ряд (2) сходится, а члены числового ряда (1), начиная с k-го, не больше соответствующих членов числового ряда (8), тогда числовой ряд (1) также сходится.

Если числовой ряд (2) расходится, а члены числового ряда (1), начиная с k-го, не меньше соответствующих членов числового ряда (2), то числовой ряд (1) расходится.

Пример.Исследовать сходимость числового ряда .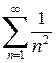

Решение.Отбросив первый член данного числового ряда (что не сказывается на его сходимости), сравним его с числовым рядом, сходимость которого уже была установлена: .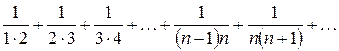

Видно, что , , ,… , .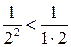

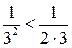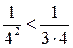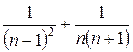Следовательно, исходный числовой ряд по признаку сравнения рядов сходится.

Пример. Исследовать сходимость ряда .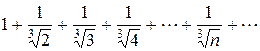

Решение.Сравним данный числовой ряд с гармоническим рядом 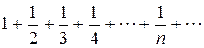, который, как известно, расходится.

Члены данного ряда не меньше соответствующих членов гармонического ряда, поэтому он также расходится.

Пример.Определить сходимость ряда .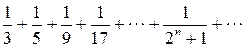

Решение.Сравним данный числовой ряд с рядом, члены которого образуют геометрическую прогрессию, т.е. 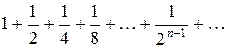, причем 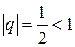, что указывает на его сходимость.

Члены данного числового ряда меньше соответствующих членов ряда геометрической прогрессии. Следовательно, по признаку сравнения данный числовой ряд также сходится.