Интегральный признак Коши.

Числовой ряд (1) с положительными невозрастающими членами, т.е. 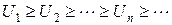, сходится или расходится одновременно с несобственным интегралом

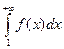, (6)

где 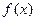– функция, определенная для всех вещественных чисел 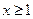, непрерывная, не возрастает и , .

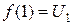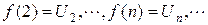Пример. Исследовать сходимость ряда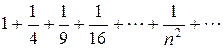

Решение.Члены данного числового ряда положительные и монотонно убывают, а 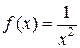. Выясним сходимость несобственного интеграла (6):

.

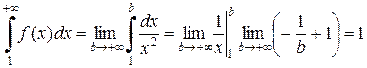Несобственный интеграл сходится, поэтому, согласно интегральному признаку Коши, данный числовой ряд сходится.

Пример. Исследовать сходимость ряда .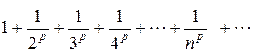

Решение.это обобщенный гармонический ряд. Члены данного числового ряда монотонно убывают.

Если 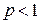, то все члены ряда, начиная со второго, будут больше соответствующих членов гармонического ряда и, согласно признаку сравнения рядов, такой ряд расходится.

Рассмотрим числовой ряд, у которого 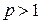. В этом случае имеем функцию 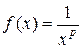и соответствующий несобственный интеграл

.

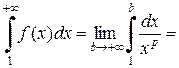
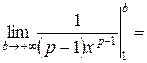
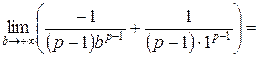
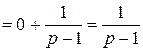Несобственный интеграл сходится, поэтому по интегральному признаку Коши данный ряд также сходится.

Пример. Исследовать сходимость ряда: .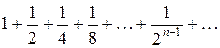

Решение.Члены данного числового ряда образуют геометрическую прогрессию, у которой первый член равен 1, а знаменатель равен .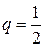

Составим функцию 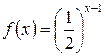и соответствующий ей несобственный интеграл

.

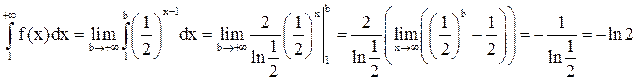Несобственный интеграл сходится, тогда по интегральному признаку Коши данный числовой ряд также сходится.

Пример. Исследовать сходимость ряда .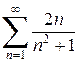

Решение.Члены данного числового ряда положительные и монотонно убывают, а 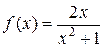. Выясним сходимость несобственного интеграла (1.3.6):

.

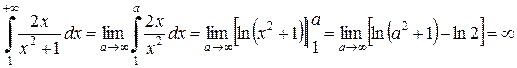Несобственный интеграл расходится, поэтому по интегральному признаку Коши данный числовой ряд также расходится.

ФУНКЦИОНАЛЬНЫЙ РЯД

Выражение

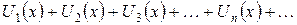(1)

называется функциональным рядом, где х вещественная переменная.

Каждый член функционального ряда (1) может быть, в частности, и постоянным при х=х₀. В этом случае функциональный ряд становится числовым. Таким образом, числовой ряд является частным случаем функционального ряда.

Функциональный ряд вида

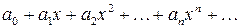(2)

или ряд более общего вида

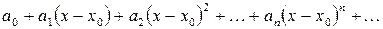, (3)

где 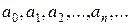не зависят от переменной х, называются степенными рядами.

Числа 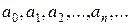называются коэффициентамистепенных рядов (2), (3).

При конкретных значениях х степенной ряд (2) (или (3)) превращается в числовой ряд, который может сходиться или расходиться.

Множество значений х, при которых числовой ряд, полученный из ряда (2) сходится, называется областью сходимости степенного ряда (2).

Теорема Абеля. Если степенной ряд (2) сходится при некотором значении 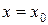, то он сходится абсолютно при всех значениях х, для которых 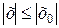. Если ряд (2) расходится при некотором значении 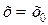, то он расходится абсолютно при всех значениях х, для которых .

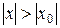Из теоремы Абеля следует, что существует такоезначение 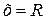, что для всех 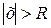степенной ряд (2) расходится, а для всех 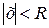степенной ряд (2) сходится.