Теорема о почленном дифференцировании степенного ряда.

Пусть степенной ряд имеет радиус сходимости R. Тогда ряд, полученный в результате дифференцирования исходного степенного ряда, также имеет радиус сходимости R, а производная суммы ряда равна сумме полученного ряда.

Пример. Найти радиус и область сходимости степенного ряда .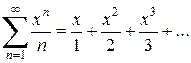

Решение.Имеем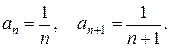Определим радиус сходимости степенного ряда по формуле (5)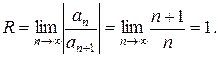

Таким образом, данный степенной ряд сходится в интервале (-1; 1).

Рассмотрим сходимость ряда на концах этого интервала.

а) Пусть 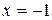. Подставив это значение в данный степенной ряд, получим следующий знакочередующийся числовой ряд 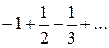., который по признаку Лейбница сходится, поскольку 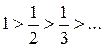и .

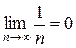б) Пусть 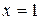. Получим знакоположительный числовой ряд 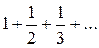. Это гармонический ряд, который, как известно, расходится.

Итак, область сходимости данного степенного ряда 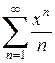представляет собой интервал [-1; 1).

Пример. Найти радиус и область сходимости степенного ряда

.

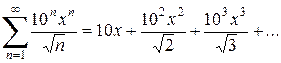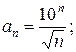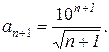Решение.По условиютогда Определим радиус сходимости степенного ряда по формуле (2.1.5)

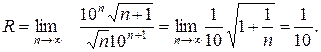
значит, интервал сходимости рассматриваемого ряда таков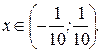

Исследуем сходимость данного степенного ряда на концах полученного интервала сходимости.

При 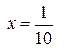имеем следующий числовой ряд 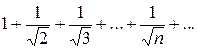. Он расходится, так как это обобщенный гармонический ряд при 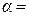0,5.

При 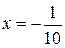имеем следующий знакочередующийся числовой ряд 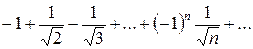, который по признаку Лейбница сходится, так

как , .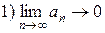

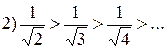Следовательно, область сходимости исследуемого степенного ряда такова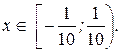

Пример. Найти радиус и область сходимости степенного ряда .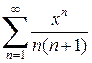

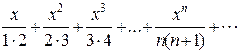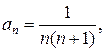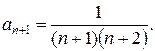Решение.Представим этот ряд в развернутом виде . Имеем тогда Определим радиус сходимости исследуемого ряда по формуле (2.1.5):

.

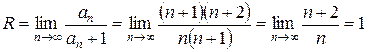Таким образом, интервал сходимости данного степенного ряда таков .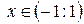

Исследуем сходимость рассматриваемого ряда на концах интервала сходимости.

При х = 1 имеем знакоположительный числовой ряд

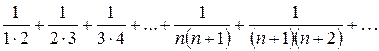. (6)

Сходимость числового ряда (2.1.6) исследуем по признаку сравнения числовых рядов. Так как в знаменателе общего члена старшая степень n равна 2, то для сравнения возьмем обобщенный гармонический ряд при 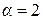, т.е.

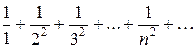, (7)

который сходится.

Сравним соответствующие члены исходного (6) и рассматриваемого (7) числовых рядов.

Имеем 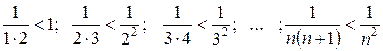. Следовательно, числовой ряд (6) по признаку сравнения сходится.

При х = - 1 получим следующий знакочередующийся числовой ряд:

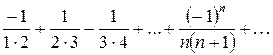. (8)

Как известно, ряд сходится, если сходится ряд, составленный из модулей членов знакочередующегося ряда. Так как при х = 1 ряд (2.1.6) сходится, то при х = - 1 ряд (8) сходится абсолютно.

Тогда область сходимости исходного степенного ряда 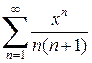представляет собой отрезок [-1;1].

Пример. Найти радиус и область сходимости степенного ряда .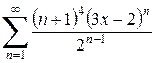

Решение.Заменим 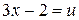. Ряд примет вид 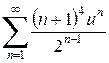. Запишем этот ряд в развернутом виде: 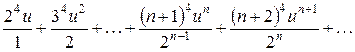. Имеем 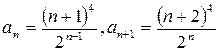. Находим радиус сходимости рассматриваемого степенного ряда по формуле (5): 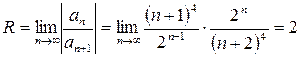. Значит, степенной ряд сходится в интервале (-2; 2).

Исследуем сходимость этого степенного ряда на концах полученного интервала сходимости. При u = 2 получим следующий числовой ряд 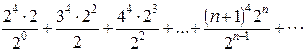или .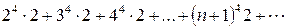

Очевидно, что n-й член полученного числового ряда не стремится к нулю при 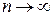, т.е. необходимое условие сходимости числового ряда не выполняется, следовательно, исследуемый числовой ряд расходится.

При u = - 2 получим следующий знакочередующийся числовой ряд

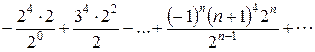или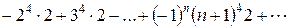

И в этом случае n-й член ряда не стремится к нулю, значит, по признаку Лейбница этот знакочередующийся ряд расходится.

Определим область сходимости исходного степенного ряда для переменной х. Поскольку 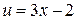, то 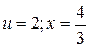при , при 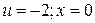, тогда область сходимости исходного степенного ряда такова .

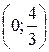Пример. Найти интервал сходимости степенного ряда .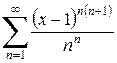

Решение. Применяем радикальный признак Коши, полагая .

Тогда ;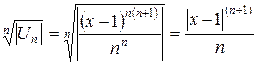

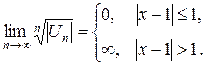
Таким образом, рассматриваемый степенной ряд сходится, если 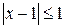, т.е. в интервале .

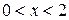КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Какой ряд называется степенным?

2. Какой ряд называется функциональным?

3. Сформулируйте теорему о почленном интегрировании степенного ряда.

4. Как найти область сходимости степенного ряда?

5. Как найти радиус ходимости?

6. Что такое числовой ряд?

7. Сформулируйте необходимое условие сходимости знакопостоянных рядов.

8. Сформулируйте признак сходимости Даламбера.

9. Сформулируйте достаточный признак сходимости Коши.

10. Сформулируйте предельный признак сравнения числовых рядов.

11. Сформулируйте признак сравнения числовых рядов.

Литература

1. Белоконь, Т.В. Математический анализ [Электронный ресурс] : методические рекомендации по организации самостоятельной работы студентов по направлениям подготовки 38.03.01 Экономика (Профили: Экономика предприятия, Международная экономика, Финансы и кредит, Банковское дело, Учет и аудит, Маркетинг, Маркетинг услуг, Рекламный бизнес, Экономико-правовое обеспечение предприятия, Бухгалтерский учет и правовое обеспечение бизнеса), 38.03.03 Управление персоналом, 38.03.06 Торговое дело, 38.05.01 Экономическая безопасность, образоват. прогр. ВПО «бакалавриат», «специалитет», оч. и заоч. форм обучения / Т.В. Белоконь, Н.С. ; М-во образования и науки ДНР, Донец. нац. ун-т экономики и торговли имени Михаила Туган-Барановского, Каф. высшей и прикладной математики. – Донецк : ДонНУЭТ, 2019. – Локал. компьютер. сеть НБ ДонНУЭТ.

2. Боронина, Е.Б. Математический анализ [Электронный ресурс] : учебное пособие / Е.Б. Боронина. – 2-е изд. – Электронные текстовые дан. – Саратов : Научная книга, 2019. – 159 c. – 978-5-9758-1745-7. – Режим доступа : http://www.iprbookshop.ru/81022.html.

3. Геворкян, Э.А. Математика. Математический анализ [Электронный ресурс] : учебное пособие / Э.А. Геворкян, А.Н. Малахов. – Электронные текстовые дан. – Москва : Евразийский открытый институт, 2010. – 344 c. – 978-5-374-00369-7. – Режим доступа : http://www.iprbookshop.ru/10715.html.

4. Гусак, А.А. Математический анализ и дифференциальное уравнение. Примеры и задачи [Электронный ресурс] : учебное пособие / А. А. Гусак. – Электронные текстовые дан. – Минск : ТетраСистемс, 2011. – 415 c. – 978-985-536-228-0. – Режим доступа : http://www.iprbookshop.ru/28122.html.

5. Кудрявцев, В.А. Краткий курс высшей математики [Текст] : учебное пособие для студентов естествен. спец. ун-тов / В. А. Кудрявцев, Б. П. Демидович. – 6-е изд. – Москва : Наука, 1986. – 576 с. : рис. + Прил.(22с.).

6. Математический анализ [Электронный ресурс] : учебное пособие / сост. Е. П. Ярцева. – Электронные текстовые дан. – Ставрополь : Северо-Кавказский федеральный университет, 2017. – 265 c. – 2227-8397. – Режим доступа : http://www.iprbookshop.ru/83227.html.

7. Математический анализ [Электронный ресурс] : электрон конспект лекций для студентов ИЭУ направлений подготовки 38.03.01 «Экономика», 38.03.06 "Торговое дело" УВ ПО «Бакалавриат», днев. и заоч. отделений, профиля «Экономика предприятия», специализация «Экономико-правовое обеспечение предприятия» / О. В. Шепеленко, С. В. Скрыпник, Т. А. Фомина [и др.] ; М-во образования и науки ДНР, ГО ВПО "Донец. нац. ун-т экономики и торговли им. Михаила Туган-Барановского", Каф. высш. и приклад. математики. - Донецк : ДонНУЭТ, 2018. - Локал. компьютер. сеть НБ ГОВПО "ДонНУЭТ".

8. Скрыпник, С.В. Математический анализ [Электронный ресурс] : учебное пособие для студентов направления подготовки 38.03.01 Экономика образоват. прогр. ВПО «бакалавриат» оч. и заоч. форм обучения / С.В. Скрыпник; М-во образования и науки ДНР, Донец. нац. ун-т экономики и торговли имени Михаила Туган-Барановского, Каф. высшей и прикладной математики. – Донецк : ДонНУЭТ, 2017. – Локал. компьютер. сеть НБ ДонНУЭТ.

9. Учебно-методическое пособие по дисциплине Математика. Математический анализ. Часть 1 [Электронный ресурс] / сост. А. В. Власов. – Электронные текстовые дан. – Москва : Московский технический университет связи и информатики, 2016. – 26 c. – 2227-8397. – Режим доступа : http://www.iprbookshop.ru/61491.html.

10. Фомина, Т.А. Математический анализ [Электронный ресурс] : учебное пособие для студентов направления подготовки 38.03.01 "Экономика"; 38.03.03 "Управление персоналом"; 38.03.06 "Торговое дело"; 38.05.01 "Экономическая безопасность", образоват. прогр. ВПО "бакалавриат", "специалитет" / Т.А. Фомина, Е.И. Сошина; М-во образования и науки ДНР, Донец. нац. ун-т экономики и торговли имени Михаила Туган-Барановского, Каф. высшей и прикладной математики. – Донецк : ДонНУЭТ, 2020. – Локал. компьютер. сеть НБ ДонНУЭТ.