ОСНОВЫ ТЕОРИИ РАЗМЕРНОСТЕЙ
Основные понятия теории размерностей
Необходимой предпосылкой теории подобия является математическое описание изучаемого процесса в виде дифференциальных или интегрирования дифференциальных уравнений и условий однозначности (граничных или начальных условий).
Из математической формулировки задачи следует перечень существенных для рассматриваемого процесса физических величин. Если перечень установлен, то выявление чисел подобия может быть произведено методом анализа размерностей.
Подробно теория размерностей рассматривается в специальной литературе. Мы ограничимся рассмотрением понятий и некоторых выводов, следу-ющих из теории размерностей.
Известно, что измерить какую-либо величину А – это значит сравнить ее с другой величиной а той же физической природы, т.е. определить, во сколько раз А больше (меньше) а. Для единообразия устанавливают определенное значение величины а и называют ее единицей измерения. Так, например, за единицу длины (метр) принимается длина 1650768,33 волн излучения атома криптона, за единицу времени (секунда) принимается определенная часть года и т.д.
Единицы измерения различных физических величин, объединенные на основе непротиворечивости друг другу, образуют систему единиц.
В настоящее время существует Международная система единицы (СИ), в которой произвольно выбраны единицы измерения так называемых первичных
(основных) величин.
В СИ в качестве первичных (основных) единиц приняты величины: массы (М), длины (L), времени (Т), силы тока (I), температуры (q), силы света (J). Здесь М, L, Т, I, q, J – называются символами соответствующих первичных величин. Эти величины характеризуют какое-либо физическое явление. Единицы измерения остальных величин выражаются через основные и называются вторичными (производными).
Формула, указывающая зависимость единицы измерения вторичной величины от первичных (основных) единиц измерения, называется размерностью.
Размерность величины указывается при помощи взятого в квадратные скобки символа этой величины.
Например, скорость v = dl/dt [v]=[L][[T*]-1, L, T – размерности длины и времени.
Размерность вторичных величин находится при помощи так называемого определительного уравнения, служащего определением этой величины в математической форме. Например, определительным уравнением для силы можно считать второй закон Ньютона F = m×a. Тогда [F] = [M][L][T]-2, для работы
А = FS, [A] = [M][L]2[T]-2.
Размерность можно представить в виде степенной формулы. Применительно к системе СИ формула размерности имеет вид
[j ] = 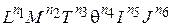 , (3.1)
, (3.1)
| где | [j] | – | вторичная производная единица измерения; |
| пi | – | действительные числа |
Размерность вторичной величины относительно данной первичной i может быть охарактеризована значением показателя степени ni при этой первичной величине. Поэтому безразмерные числа часто называют величинами с нулевой размерностью, т.к. для них все показатели степени в формуле размерности (3.1) равны нулю.
В учении о размерностях различают также размерности независимых и
зависимых величин.
Если среди п физических величин u1 , и2, …, иi , ui+1,…, un часть величин u1 , и2, …, иi обладают тем свойством, что размерность каждой из них не может быть представлена из размерностей остальных рассматриваемых величин, то размерности [u1], [и2],…, [иi] называются независимыми. Размерности же остальных величин, т.е. [ui+1], [ui+2],…, [un ], могут быть выражены, как функции независимых размерностей, т.е.
[ui+1] = j i+1 ([u1], [и2],…, [иi]);
[ui+2] = j i+2 ([u1],…, 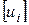 );
……………………………..
[uп] = j п([u1],…, );
……………………………..
[uп] = j п([u1],…, 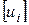 ). ).
|
В этом случае размерности [ui+1],…, [un ] называются зависимыми.
При рассмотрении большинства задач очень редко бывает, что одновременно исследуются все шесть основных единиц измерения (3.1), так, если изучаются чисто механические задачи, то ампер, градус Кельвина, свеча не входят в размерность ни одной величины, т.к. размерности вторичных величин выражаются через метр, килограмм, секунду.
При решении конкретных задач зачастую возникает вопрос, можно ли переходить от одних единиц измерения к другим. Для этого рассмотрим пример механической системы, которая имеет три первичных (основных) единицы измерения. Общность получаемых ниже выводов от этого не теряется.
В качестве первичных величин можно выбрать какие-либо иные, чем [L], [M], [T], например, и1, и2, и3 , в том случае если:
а) размерности [u1], [и2], [и3] являются независимыми функциями [L], [M], [T], т.е. [u1] ¹ [и2]a [и3]b при любых a и b; 
б) возможно однозначное обратное преобразование, т.е. [L], [M], [T] единственным образом можно выразить через [u1], [и2], [и3].
Покажем, при каком условии оба эти требования удовлетворяются. Для
этого предположим, что ui (i = 1, 2, 3) имеют следующие размерности
[u1] = [M] 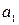 [L]
[L] 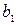 [T]
[T] 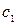 , [u2] = [M]
, [u2] = [M] 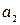 [L]
[L] 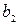 [T]
[T] 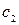 , [u3] = [M]
, [u3] = [M] 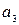 [L]
[L] 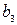 [T]
[T] 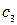 (3.2)
(3.2)
Такая система уравнений, как известно из курса алгебры, имеет решение и при том единственное, если составленный из коэффициентов уравнения определитель отличен от нуля, т.е.
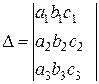 ¹ 0. (3.2)
¹ 0. (3.2)
Тем самым удовлетворяется требование «б», т.е. при выполнении условия (75) [L], [M], [T] единственным образом выражаются через [u1], [и2], [и3].
Условие (82) указывает в то же время на независимость функций иi . Действительно, если бы имело место равенство
[u1] = [и2]a [и3]b ,
откуда
lg [u1] = a lg [u2] +blg [u3],
то тогда
а1 = aа2 +bа3; b1 = ab2 +bb3; c1 = ac2 +bc3,
т.е. первая строка определителя являлась бы линейной комбинацией второй и третьей, и определитель равнялся бы нулю, что противоречит условию (3.2).
Например, первичными величинами могут быть сила, время, длина, т.е.
и1 = F, и2 = T, и3 = L
[u1] = [M]1[L]1[T]-2, [u2] = [M]0[L]0[T]1, [u3] = [M]0[L]1[T]0,
Определитель такой системы
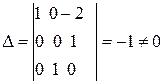 ,
,
т.е. удовлетворяется условие (3.2).
Рассмотрим примеры использования метода размерностей:
1. Ламинарное движение вязкой жидкости в круглой трубе.
Из гидродинамики известно, что объемный расход жидкости описывается уравнением
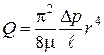 , (а)
, (а)
| где | Q | – | объемный расход жидкости; |
| m | – | коэффициент вязкости жидкости; | |
| Dр | – | падение напора на участке длины 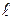 ; ;
| |
| r | – | радиус трубы. |
Приведем уравнение (а) к безразмерному виду. С другой стороны
Q =pr2v, (б)
где v – среднее значение скорости по сечению трубы. Тогда
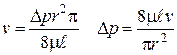 . (в)
. (в)
Введя в (в) масштабные преобразования
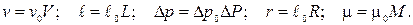 (г)
(г)
Получим
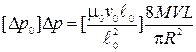 . (д)
. (д)
Чтобы получить уравнение в безразмерном виде, нужно принять
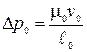 . (е)
. (е)
Полученное равенство называется уравнением связи между масштабом и намечает определенное ограничение на свободу выбора масштабов.
Так как получено одно уравнение связи, а число масштабов четыре, то три из них можно выбрать, а один определить, пользуясь уравнением связи между масштабами.
Приняв, 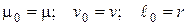 , получим Dр0 = mv/r и значение безразмерных величин
, получим Dр0 = mv/r и значение безразмерных величин
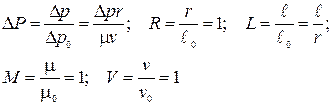

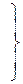 . (ж)
. (ж)
После этого выражение (д) примет вид
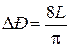 . (3)
. (3)
Следовательно, выражение (а), включающее пять размерных величин, преобразовано в выражение (3), состоящее из двух безразмерных величин. При этом соотношение между масштабами подобия определяется зависимостью
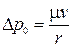 . (и)
. (и)
2.Дифференциальное уравнение изгиба изотропной пластины под
действием равномерно распределенной нагрузки q
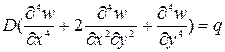 . (А)
. (А)
Введем безразмерные величины и обозначения
w = LW, x = LX, y = BY, 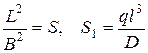 . (Б)
. (Б)
Подставляя (Б) в (А), получим
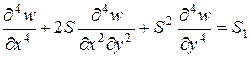 (В)
(В)
Таким образом, уравнение (А), имеющее пять размерных величин 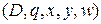 преобразовано в выражение (В), состоящее из двух безразмерных величин: комплекса
преобразовано в выражение (В), состоящее из двух безразмерных величин: комплекса 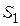 и симплекса
и симплекса 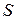 .
.
Дата добавления: 2017-10-04; просмотров: 4181;











