Метод эквивалентных материалов

Этот метод применяют для исследования вопросов, связанных с проявлением горного давления в очистных подготовительных выработках при разработке месторождений полезных ископаемых; в подземных капитальных выработках; при изучении вопросов, связанных с породами, сдвижения массивов и других физических процессов, происходящих в массивах в связи с проведением в них горных работ.

Изучение всех этих вопросов аналитическим методом и непосредственно на практике связано с большими трудностями, поэтому использование метода моделирования имеет большое теоретическое и практическое значение.

В предвоенные годы во ВНИМИ Г.Н. Кузнецовым был разработан метод моделирования, в основу которого была положена идея создания моделей горных массивов из искусственных материалов, эквивалентных по своим деформационным и плотностным свойствам горным породам при принятом масштабе моделирования. Сейчас этот метод широко используется под названием МЭМ.

Сущность метода эквивалентных материалов заключается в том, что на физических моделях с известными допущениями и при соблюдении условий подобия изучают интересующие нас физические процессы и результаты этих исследований используют для разработки теории «механизма» процесса, а также для разработки практических рекомендаций для промышленности. Например, МЭМ широко применяют для изучения процесса сдвижения пород массива при очистной выемке полезных ископаемых (рис. 4.1).

Рис. 4.1. Схема к моделированию задачи деформаций горных пород
на эквивалентных материалах: а – образец; б – модель.

При достаточном удалении от штреков характер проявления давления горных пород на крепь во времени будет изменяться только в направлении движения очистного забоя. Следовательно, задача изучения давления пород в очистных выработках сводится к плоской и рассматривается для сечения А–А. На плоской модели (рис. 4.1, б) с соблюдением условий подобия воспроизводится процесс выемки полезного ископаемого, в результате которого в модели происходит процесс сдвижения пород, подобный натуре.

В основе метода лежит теория механического подобия Ньютона, которая предполагает геометрическое, кинематическое и динамическое подобия.

Геометрическое подобие. Обеспечивается в том случае, если все линейные размеры, как и ранее, будут уменьшены в определенное постоянное число раз по сравнению с той областью натуры, в которой изучается данное явление, т.е.

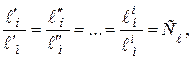(4.1)

где 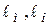– линейные размеры модели и натуры, соответственно.

Кинематическое подобие будет обеспечено в том случае, если сходственные частицы, двигаясь по геометрически подобным траекториям, проходят геометрически подобные пути в промежутки времени, отличающиеся постоянным множителем, т.е.

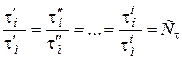. (4.2)

Динамическое подобие имеет место в том случае, если массы двух сходственных частиц (соответствующим образом расположенных в пространстве и времени) отличаются друг от друга в одно и тоже число раз

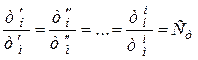. (4.3)

Выразив в равенствах (4.3) массу через объем и плотность, получим

(4.4)

или

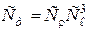, (4.5)

где 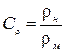. (4.6)

Так как множитель подобия 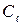задан геометрическим подобием, то для соблюдения условий динамического подобия достаточно задать соотношение плотностей, т.е. С_r. Из условия механического подобия 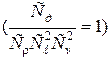, выражая множители подобия через соответствующие соотношения и произведя преобразования, будем иметь

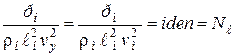(инвариант подобия Ньютона) (4.7)

Следовательно, определив параметры модели, при которых соотношения множителей подобия удовлетворяют условию (4.7, мы получим модель, динамические процессы в которой будут подобны соответствующим процессам в натуре.

Обращаясь к конкретной задаче о давлении пород на крепь подземной выработки, установим критерии подобия и множители подобия для моделирования указанного процесса методом ЭМ.

На основании вышеизложенного выделим основные силы, которые определяют характер физического процесса.

В первом приближении можно ограничиться учетом двух родов сил, а именно: внешних сил – тяжести и внутренних сил – напряжений, возникающих в породе.

Преобразуем формулу (4.7), выражающую общий закон подобия Ньютона для случая совместного действия сил тяжести и внутренних напряжений. Заменяя в ней значения квадратов скоростей через ускорения и длины, получим

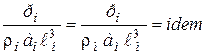(4.8)

В данном случае деформация и разрушение породы происходит за счет действия сил тяжести, т.е. а = .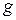

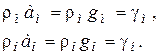(4.9)

где g – объемный вес материала.

Введем в (108) обозначение

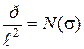, (4.10)

под которым подразумеваем предельные напряжения: на растяжение, сжатие,

сдвиг или деформационные характеристики пород.

Подставив зависимости (4.9), (4.10 в (4.8), получим

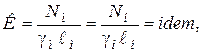(4.11)

где К – безразмерное число, являющееся определяющим критерием подобия.

На основании полученного выражения можно установить основные требования к модели, обеспечивающие механические подобия явления. Если модель изготовить из материала натуры, то будем иметь одинаковые физико-механические свойства и натуры: N_м = N_н; g_м = g_н.

Однако смысл модулирования в данном случае заключается в том, чтобы

геометрические размеры модели были меньше размеров натуры, т.е. .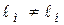

В этом случае равенство (4.11) не имеет места. Для сохранения условий его инвариантности следует полагать, что N_м = N_н; g_м ¹ g_н или N_м ¹ N_н;
g_м ¹ g_н..

В первом случае согласно (4.11)

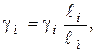(4.12)

т.е. объемный вес материала модели должен быть значительно больше объемного веса материала натуры.

Во втором случае

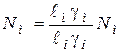(4.13)

Зная механические свойства материала натуры и задаваясь соотношениями 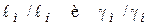, получим значения механических свойств материала модели, которые необходимы для обеспечения подобия модели и натуры.

При изучении процесса разрушения пород в качестве определяющих характеристик механических свойств пород должны быть взяты предельные значения прочности породы при ее разрушении, которые могут быть определены путем построения огибающей кругов Мора.

Таким образом, при подборе материалов-эквивалентов в качестве определяющих характеристик прочности пользоваться совокупностью значений временного сопротивления пород на сжатие R_с и растяжения R_р или же совокупностью значений коэффициента сцепления С_о и угла внутреннего трения tgj. В этом случае необходимо соблюдать следующие равенства:

условие подобия внешних сил

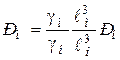(4.14)

условие подобия процессов разрушения

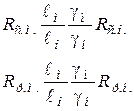
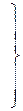(4.15)

или

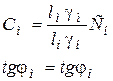
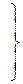. (4.16)

Для подобия процессов механики горных пород в области упругих деформаций соблюдаются равенства

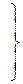, (4.17)

где Е – модуль упругости; m– коэффициент Пуассона.

Для подобия механических процессов в массиве горных пород в области пластических деформаций во всем диапазоне напряжений начальных до разрушающих без учета влияния времени должно быть соблюдено условие

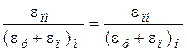. (4.18)

При этом

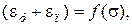
где e_п,e_у – пластическая и упругая относительные деформации.

Достоинством метода эквивалентных материалов следует считать возможность воспроизводить процессы неупругого деформирования и разрушения пород массива вблизи горных выработок. Необходимо также отметить, что этот метод позволяет строить объемные модели и на их основе решать трехмерные задачи петромеханики.

Указанные обстоятельства способствовали широкому внедрению метода

эквивалентных материалов в лабораторную практику: более 150 конкретных задач горной механики решено на моделях из эквивалентных материалов, причем около 30 из них – на объемных моделях.

В то же время методу моделирования на эквивалентных материалах присущи серьезные недостатки.

1. Широкий диапазон физико-механических свойств пород, слагающих моделируемый массив, трудно воспроизвести на каком-либо типе эквивалентных материалов только за счет изменения его состава, поэтому при построении модели исследователь вынужден прибегать к целому ряду эквивалентных материалов, отличающихся по своим исходным компонентам и физико-математическим свойствам, что усложняет постановку эксперимента.

2. В большинстве случаев при изготовлении модели оказывается затруднительным, а иногда и вовсе невозможным выполнить условия подобия внешних сил, процессов разрушения и процессов деформирования (упругого и пластического) так как указанные условия подобия механических характеристик модели и натуры должны удовлетворять равенствам

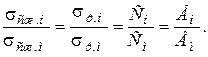(4.19)

3. Изучение деформационных процессов в окружающем выработки массиве требует сооружения моделей внушительных размеров, что сопровождается значительным повышением трудоемкости самого эксперимента.

4. Достоверность и репрезентативность результатов, полученных на моделях из эквивалентных материалов, в значительной степени зависит от технологии изготовления, поэтому даже при правильно подобранных компонентах возможны существенные погрешности.

5. Модель, обеспечивающая удовлетворительную сходимость с натурой при изучении медленно протекающих процессов, не может быть использована для моделирования динамических процессов в горном массиве в силу невыпол-

нения всех условий подобия.

6. Закладка динамометров в модель для измерения напряжений зачастую приводит к искажению напряженно-деформационного состояния изучаемого массива.

7. Измерение смещений на мелкомасштабных моделях не может быть выполнено с достаточной точностью, т.е. чувствительность серийных измерительных устройств не обеспечивает требуемую точность измерения смещений отдельных точек массива с учетом принятого масштаба.

Моделирование на эквивалентных материалах позволяет с большой степенью детальности проследить механизм процессов в толще пород при движении забоя выработки, особенно процессов деформирования пород с разрывом сплошности, что обычно исключено при других методах моделирования. Вследствие этого метод эквивалентных материалов является наиболее действенным, благодаря чему он получил широкое применение при решении различных задач механики горных пород.

Одним из преимуществ метода моделирования на эквивалентных материалах является возможность измерения показателей, отражающих напряженно-деформированное состояние (НДС) массива в интересующих областях, которые в натурных условиях осуществить практически невозможно ввиду труднодоступности участков массива.

При условии удовлетворения всех критериев подобия для эквивалентных материалов и обеспечении геометрического подобия натуры и модели, совпадение механических процессов может быть обеспечено при подобии граничных условий.

В принципе, модель достаточно полно отражает НДС массива в натуре. Соблюдение же граничных условий по торцам модели не представляется возможным, однако, в силу известного принципа Сен-Венана, можно утверждать, что роль торцов становится заведомо малой на расстояниях от них, равных толщине модели. Поэтому при отработке моделей замеры величин смещений кровли и давления на крепь являются достоверными только в ее средней части.

Лабораторный подбор и испытания эквивалентного материала для изготовления моделей направлены в сторону изыскания удобно обрабатываемых смесей, которые не обладали бы длительными сроками схватывания и твердения, а по своим физико-механическим свойствам обеспечивали бы подобие с горными породами. При этом безразмерные константы – коэффициенты Пуассона и углы внутреннего трения должны численно совпадать в эквивалентном мате­риале и натурных горных породах.

По природе связующих веществ, применяемые в настоящее время, эквивалентные материалы разделяются на четыре группы:

1. На основе углеводородов нефтяного происхождения (вазелин, парафин, масла и др.) – обладают пластичными и упругопластичными свойствами.

2. На основе неорганических гидравлических связующих (цемент, гипс, жидкое стекло, тиосульфат натрия) – обладают хрупким характером разрушения, а при добавлении в состав глины приобретают пластичные свойства.

3. На основе синтетических полимеров (эпоксидная, карбомидная, кремнийорганическая и др. смолы) – обладают упруго-пластичными и хрупкими свойствами.

4. На основе смол естественного происхождения (пек, канифоль и др.) – обладают свойствами хрупких материалов.

В последние годы все более популярным становится также моделирование на кусочках пиленого сахара, который дает хорошие качественные результаты.

При подборе эквивалентных материалов с конкретными свойствами используют различные модификаторы, присадки и инертные заполнители. В качестве последних применяются мелкие кварцевые пески и мелкодисперсные материалы (цемент, мел, инертная пыль, порошки солей металлов и др.). Подобрав и уточнив рецептуры эквивалентных материалов для всей моделируемой толщи, приступают к следующему этапу - изготовлению самой модели.

Модели изготавливают непосредственно в испытательных стендах, представляющих собой жесткие рамные металлические конструкции. Для изготовления и испытания плоских моделей, выполненных в разрезе по простирнию перпендикулярно к плоскостям напластования, слоистости или полосчатости моделируемой толщи, применяют стенды, подобные представленному
на рис. 4.2.

Если необходимы плоские модели, выполненные для наклонного залегания пород в разрезе вкрест простирания, применяют поворотные (круговые) стенды. Для объемных моделей служат трехмерные поворотные стенды.

В зависимости от решаемых задач моделирование ведут в различных геометрических масштабах: мелких, от 1:400 до 1:100, или крупных, от 1:60 до 1:10. Толщи слабых пород моделируют только в крупных масштабах.

Разделение толщи пород в модели на отдельные слои обеспечивают путем присыпки поверхности каждого слоя крупной молотой слюдой, трещиноватость или кливаж воспроизводят насечкой свежеприготовленных слоев до отвердения или схватывания материалов.

При изготовлении плоских моделей вместо опалубки используют прозрачные ограждающие стенки, стационарно закрепляемые на весь период испытания модели. Для этих целей применяются листовые закаленные стекла, укрепляемые на стыках швеллерами, которые обеспечивают необходимую жесткость прозрачного бокового ограждения. После изготовления модели и набора эквивалентным материалом прочности (или его остывания) на поверхность моделируемого массива наносится мерная сетка, в намеченных слоях устанавливают марки и датчики для регистрации картины поля напряжений, деформаций и смещений в период испытания, а также выполняются полости, имитирующие горные выработки, в которые встраиваются приборы, воспроизводящие работу крепи.

Напряженное состояние и деформации элементов модели определяют также с помощью спаренных микроскопов, жестко соединенных между собой и позволяющих определять с высокой точностью смещения двух точек относительно друг друга. База измерений в моделях указанными выше приборами составляет 40…50 мм, а относительная погрешность 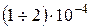, т. е. на порядок ниже, чем при измерениях в натуре.

Для определения сдвижений точек плоской модели в процессе ее испытания служит метод фотофиксации – периодическое фотографирование боковой поверхности модели с установленными в ней марками и последующие измерения смещений марок на фотоснимках, осуществляемые на компараторе. Метод фотофиксации позволяет быстро и одновременно регистрировать смещения всех точек на боковой поверхности модели, но точность определения смещений точек модели, учитывая масштаб моделирования, оказывается обычно ниже точности определения смещений соответствующих точек при измерениях не­посредственно в натурных условиях. Установка на боковой поверхности модели блочных тензометров позволяет повысить точность определения смещений точек методом фотофиксации в 20 раз. При масштабе фотоснимка 1:10 и геометрическом масштабе модели 1:100 значения сдвижений точек в пересчете на натуру могут быть определены в этом случае с точностью до 1 мм. Такую же точность определения смещений обеспечи­вают зеркальные и оптические тензометры, при этом смещения реперов в увеличенном виде фиксируют на экране.

Для воспроизведения работы крепей применяют приборы пьезометрического и рычажного типов – для моделей мелких масштабов, рычажно-маятникового и гидравлического типов – для моделей крупных масштабов.

Завершающим этапом моделирования является собственно испытание модели, т.е. воспроизведение в определенном масштабе времени процесса изменений полей напряжений, деформаций и смещений с разрывом сплошности при разработке. Исходя из конкретной задачи, при испытании модели более подробно изучают распределение напряжений в массиве вокруг забоя выработки, либо развитие деформаций и сдвижений толщи пород и земной поверхности, либо развитие деформаций, разрушений и смещений пород в призабойном пространстве и взаимодействие пород с крепью и т. д.

На рис. 4.3 показаны виды некоторых моделей из эквивалентного материала с различными вариантами решаемых исследователями задач.

По окончании испытания модели обычно из ее части, не подвергнутой деформациям при испытаниях, вырезают образцы материалов-эквивалентов для проведения контрольных определений их свойств.

Обработка результатов исследований производится путем построения функциональных зависимостей изучаемых параметров от изменения горно-геологических и горнотехнических условий. Они представляются в виде относительных показателей, при этом полученные в результате зависимости должны сопоставляться с результатами натурных исследований.

а)

б)

в)

Рис.4.3. Некоторые варианты моделей из эквивалентных материалов,
выполненные на различных стендах: а) – изучение характера смещений толщи пород над выработанным пространством; б) – изучение характера смещения пород вокруг забоя подготовительной выработки пересекающей трещину;
в) – изучение характера деформирования приконтурного массива в окрестности одиночной выработки, закрепленной металлической арочной крепью с обратным сводом.

Для построения прогнозных зависимостей серии опытов планируют так, чтобы максимально охватить все необходимые условия и получить надежные результаты, для чего используют современные научные методы планирования экспериментов, например, метод латинских квадратов.