Определение вида критериев с помощью анализа размерностей

При физическом моделировании функциональная зависимость между переменными и параметрами, характеризующими рассматриваемый процесс, часто бывает неизвестной. В этом случае определение критериев-комплексов П и критериев-симплексов S может быть осуществлено с помощью анализа размерностей. В основу этого метода положены два допущения.

Пусть при исследовании какого-либо физического процесса необходимо установить зависимость какой-либо физической переменной от всех существенных для данного процесса переменных параметров.

Будем считать, во-первых, что заранее известно, от каких параметров и переменных зависит указанная физическая переменная, и, во-вторых, что между всеми существенными для рассматриваемого процесса величинами имеет место степенная функциональная связь.

Оба допущения существенно снижают принципиальную и практическую ценность метода анализа размерностей. Действительно предположение о том, что любая важная для какого-либо физического процесса переменная представляет собой степенную функцию от остальных параметров и является в значительной мере произвольным. Что же касается первого допущения, то оно по существу означает утверждение о далеко идущих знаниях механизма изучаемого процесса.

Метод анализа размерностей также не дает никаких указаний для составления перечня переменных и параметров, существенных для рассматриваемого процесса. Ответственность за составление такого перечня каждый раз ложится целиком на исследователя. Поэтому одна или несколько из существенных для процесса величин могут быть опущены, что легко может привести к неверным результатам.

Сущность метода анализа размерностей целесообразно пояснить на конкретном примере.

Рассмотрим гидравлическое сопротивление, возникающее при течении вязкой жидкости внутри круглой трубы. В соответствии с первым допущением будем считать, что падение давления 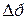на участке трубы длиной 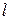зависит от средней скорости жидкости 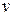, диаметра трубы 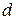, длины рассматриваемого участка 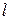, плотности жидкости 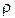и от ее коэффициента вязкости 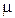, т.е.

.

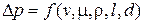В соответствии со вторым допущением 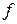есть степенная функция, т.е.

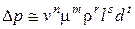, (А)

причем 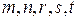– некоторые показатели степени, выбор которых вначале ничем не ограничен.

Размерности величин, входящих в соотношение (А), будут:

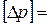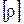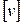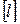кгс/м², = кгс²/м⁴; =м/с; =м; 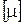= кгс·с/м²; 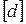= м.

Подставив в соотношение (А) указанные размерности, получим

кгс/м²=(м/с)^п(кгс·с/м²)^т(кг·с²/м⁴)^r(м)^s(м)^t. (Б)

Размерности обеих частей соотношения (Б) должны быть одинаковыми. Поэтому, приравняв в соотношении (Б) показатели степени при одинаковых основных размерностях (кг, м, с), получим:

(кг) 1=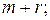

(м) – 2 = 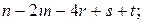(В)

(с) 0 = – .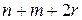

Система из трех уравнений (В) содержит пять неизвестных величин 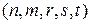. Решая эту систему относительно показателей 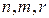, находим для них следующие выражения:

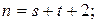
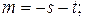(Г)

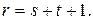
Подставив выражение (Г) в выражение (А), получим

.

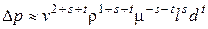Отсюда

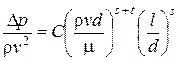, (Д)

где 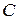– безразмерный множитель пропорциональности.

Безразмерные величины

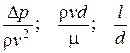
представляют собой искомые выражения для критериев. Число последних находится в полном соответствии с Пи-теоремой. Действительно, общее число 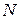величин, входящих в выражение (А), равно

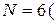т.е. .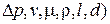

Число 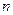величин с неодинаковыми размерностями составляют

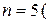т.е. .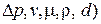

Число же 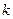величин с независимыми размерностями

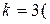т.е. .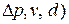

Поэтому, согласно Пи-теореме число критериев-комплексов должно быть

.

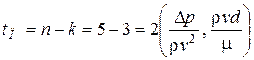Число критериев-симплексов

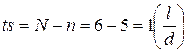
и общее число критериев

.

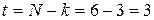Как видно из изложенного, значения показателе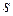й и 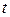, а также множителя 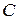остались неизвестными. Они могут быть определены опытным путем, разумеется при условии, что между критериями, входящими в уравнение (Д), существует степенная функциональная связь.

Необходимо отметить, что при исследовании физических процессов с использованием метода анализа размерностей возможны грубые ошибки. Причины таких ошибок заложены в самом методе анализа размерностей, не дающем никаких указаний относительно того, какие переменные и параметры являются существенными для того или иного изучаемого процесса. Неучет одного существенного параметра может привести исследования к значительной ошибке.

В этом отношении метод, основанный на анализе дифференциальных

уравнений математической физики и соответствующих начальных и краевых условий, свободен от недостатков, присущих методу анализа размерностей. Особенно отчетливо сказываются преимущества метода анализа дифференциальных уравнений в сочетании его с масштабными преобразованиями.

Эффективность методов теории размерностей покажем на примере определения масштаба времени при моделировании реологических процессов. Прежде всего, необходимо обратить внимание на то, что до сих пор не выработано обоснованное общее решение, касающееся определения масштаба времени.

Так, в задачах фотоползучести принимается уравнение линейно-наследственной ползучести Больцмана-Вольтерра и определяются реологические параметры 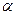и 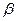уравнений состояния моделей и натуры, на основании чего вычисляется масштаб времени

,

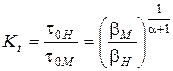где 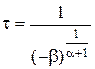– время ретардации (последствия), принимаемое за единицу измерения.

При использовании метода эквивалентных материалов масштаб времени определяется из условия кинематического подобия:

.

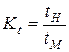Рассмотрим задачу о смещении контура горной выработки, подверженной влиянию очистных работ в зависимости от следующих определяющих параметров:

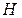– глубина разработки (места заложения выработки);

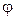– угол падения вмещающих пород;

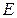– модуль упругости вмещающих пород;

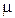– коэффициент Пуассона пород;

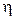– коэффициент динамической вязкости боковых пород;

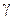– объемный вес пород вышележащей толщи;

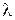– коэффициент бокового распора ;

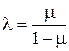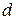– характерный геометрический размер сечения выработки;

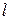– расстояние от контура выработки до очистного забоя;

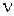– скорость подвигания очистного забоя;

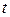– время.

Представим величину смещения контура выработки как функцию всех перечисленных параметров:

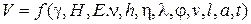. (3.3)

Все величины, входящие в зависимость (3.3), за исключением 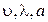, обладают определенной размерностью. Как известно, размерность любой физической величины можно представить в виде произведения возведенных в степень размерностей некоторых основных величин. Для поставленной задачи достаточно принять единицу длины 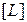, единицу массы 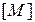и единицу времени 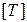. Заметим, что в качестве основных величин можно выбрать и любые другие, но при этом должны выполняться два условия:

а) размерности новых величин должны быть независимыми функциями

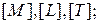
б) должно выполняться обратное преобразование 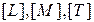через новые величины единственным образом.

В качестве основных величин примем 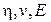и выразим их размерности через основные единицы СИ.

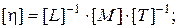
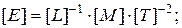(3.4)

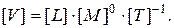
Для выполнения указанных выше требований достаточно, чтобы определитель, составленный из показателей степеней, был отличен от нуля. В нашем случае будем иметь

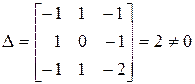(3.5)

Следовательно, условия независимости и обратного преобразования выполняются.

Функциональную зависимость (3.3) между величинами, характеризующими процесс конвергенции контура выработки можно представить в виде зависимости между составленными из них безразмерными комплексами. При этом учтем, что 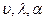являются безразмерными, а 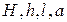– имеют одинаковую размерность. Очевидно зависимость (3.3) может быть представлена следующим образом:

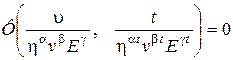(3.6)

или

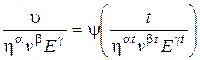. (3.7)

Получено два критерия подобия. Таким образом, задача свелась к нахождению зависимости между двумя величинами, характеризующими процесс смещения контура выработки. Это геометрические параметры рассматриваемой выработки и время.

Для определения неизвестных показателей степеней при 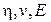воспользуемся выражениями (3.4) и (3.7)

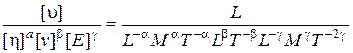, (3.8)

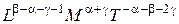, (3.9)

откуда получаем систему уравнений

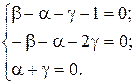(3.10)

Решив систему уравнений (3.10), получим

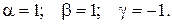
Следовательно, один из критериев подобия имеет вид:

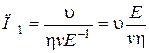. (3.11)

Аналогично находим второй критерий подобия

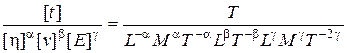, (3.12)

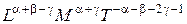, (3.13)

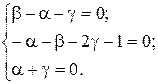(3.14)

Из решения системы (3.14) получим следующие значения показателей степени

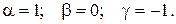
Следовательно, второй критерий подобия

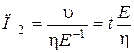. (3.15)

Учитывая зависимость (3.7) запишем:

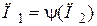. (3.16)

Очевидно, условие подобия модели и натуры будет соблюдено при

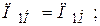
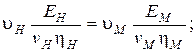(3.17)

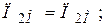
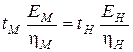. (3.18)

Из последнего равенства определяется масштаб времени при моделировании

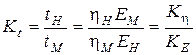. (3.19)

Из формулы (3.17) аналогично определяется масштаб скорости при условии, что геометрический масштаб моделирования задан

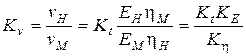. (3.20)

Полученные критерии подобия (3.11) и (3.15) действительно являются безразмерными комплексами.

Результаты и выводы, полученные в этом примере, соответствуют, так называемой, Пи-теореме и теоремам подобия.

ПИ-теорема

Впервые доказательство Пи-теоремы было опубликовано в 1912 г. в трудах аэродинамического института, возглавляемого русским ученым Н.К.Жуковским.

Пи-теорема формулируется следующим образом: всякое уравнение, связывающее между собой N физических величин, среди которых к величин обладают независимыми размерностями, может быть преобразовано в уравнение, связывающему N-к безразмерных комплексов и симплексов (отношение двух одноименных величин) составленных из этих величин.

Согласно Пи-теореме, из N размерных величин, связанных физическим уравнением, можно составить не более N-к независимых безразмерных комплексов и симплексов. Доказательства теоремы или ее пояснение не приводим, ввиду их громоздкости.

Теоремы подобия

Основные положения теории подобия формулируют в виде трех теорем.

Первая теорема подобия устанавливает связь между константами подобия и позволяет выявить критерии подобия. В общей форме эту теорему формулируют так: подобные между собой процессы имеют одинаковые критерии подобия.

Например, для первого процесса имеем критерии

.

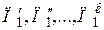Аналогично для второго процесса имеем

.

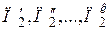Для подобных явлений должно соблюдаться равенство одноименных критериев подобия

.

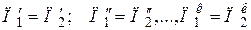Вторая теорема подобия устанавливает возможность представления интеграла как функции от критериев подобия дифференциального уравнения. На основании этой теоремы любая зависимость между переменными, характеризующими какое-либо явление 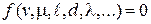, может быть представлена в виде зависимости между критериями подобия

.

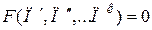Зависимость такого типа называется обобщенным или критериальным уравнением. Так как для всех подобных между собой явлений критерии подобия сохраняют одно и то же значение, то и критериальные зависимости для них одинаковы. Следовательно, представляя результаты какого-либо опыта в критериях подобия, мы получим обобщенную зависимость, которая справедлива для всех подобных между собой явлений. Помимо критериев подобия в
критериальные уравнения могут входить также симплексы – безразмерные отношения однородных физических величин.

Третья теорема подобия устанавливает условия, достаточные и необходимые для того, чтобы процессы были подобны. Подобны те процессы, условия однозначности которых подобны, и критерии, составленные из условий однозначности, численно одинаковы.

Задача исследования какого-либо физического процесса по существу может считаться ращенной, если найдены функции, описывающие поля всех характерных для рассматриваемого процесса физических переменных. Однако, пользуясь одними только законами физики, невозможно без промежуточных математических операций описать протекание рассматриваемого процесса в любой момент времени во всем изучаемом пространстве. В связи с этим изучение процесса производится вначале не во всем пространстве, которое охвачено исследуемым процессом, и не за конечный промежуток времени, а в произвольно выделенной «материальной точке» и в течение элементарного промежутка времени. При этом материальная точка должна представлять собой объем, размеры которого настолько малы по сравнению с размерами всего изучаемого пространства или объема, что они могут рассматриваться как дифференциалы длины dx, dy, dz, т.е. материальная точка представляет собой элементарный параллелепипед, являясь «микрокосмосом» по отношению ко всему изучаемому пространству, и в то же время должен быть «макрокосмосом» по отношению к молекулам. Это означает, что число молекул, находящееся в параллелепипеде, должно быть очень велико, а размеры dx, dy, dz должны быть достаточно велики по сравнению с молекулярными расстояниями.

Эти требования обычно легко удовлетворяются. Элементарный промежуток времени также должен быть достаточно малым, чтобы можно было считать, что на его протяжении в пределах материальной точки находятся одни и те же молекулы. Этому требованию удовлетворяет промежуток времени, равный дифференциалу dt.

Таким образом, промежуток времени dt и объем 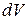, в пределах которых рассматривается изучаемый процесс, являясь математической точки зрения физики величины, достаточно большие (что позволяет среду, в которой протекает физический процесс, рассматривать как континуум).

Выбрав, таким образом, в качестве объекта первоначального исследования элементарный объем, формулируют для него соответствующие законы или принципы физики. В результате получается одно или система дифференциальных уравнений математической физики, которые устанавливают взаимосвязь между пространственно-временными изменениями всех физических переменных. Эта система уравнений описывает все без исключения явления одного класса независимо от геометрической конфигурации изучаемого тела, а также независимо от физических свойств и условий его взаимодействия с окружающей средой.

Чтобы из целого класса выделить единичный процесс, определить его однозначно, необходимо к дифференциальным уравнениям присоединить математическое описание всех частных особенностей, которые называются условиями однозначности. Эти условия определяются заданием:

1) геометрических условий, характеризующих форму и размеры тела, в котором протекает процесс;

2) физических условий, характеризующих физические свойства среды и тела;

3) граничных условий, характеризующих особенности протекания процесса на границах тела;

4) временных условий, характеризующих особенности протекания процесса во времени.

Условия 3) и 4) называют еще краевыми условиями.

Условия однозначности могут быть заданы в виде числового значения или в виде дифференциального уравнения.

После приведения дифференциальных уравнений, начальных и граничных условий к безразмерному виду и задания численных значений безразмерных параметров получают систему уравнений, которые охватывают уже не единичные процессы, а целую группу процессов.