Подобие физических явлений
Понятия подобия может быть распространено на любые физические процессы. Можно говорить, например, о подобии движения тел или потоков жидкости; о подобии сил, вызывающих подобные между собой движения; о подобии температур и тепловых потоков и т.д. Однако, чтобы использовать понятие подобия, необходимо знать условия подобия рассматриваемых явлений.
1. Понятие подобия физических явлений применимо только к явлениям одного и того же рода, которые качественно одинаковы и аналитически описываются одинаковыми уравнениями, как по форме, так и по содержанию. Если же аналитические описания двух каких то явлений одинаковы по форме, но различны по физическому содержанию, то такие явления называются аналогичными. Такая аналогия существует, например, между явлениями теплопроводности и диффузии.
2. Обязательной предпосылкой подобия физических явлений должно быть геометрическое подобие, т.е. подобные явления протекают в геометрически подобных системах.
3. При анализе подобных явлений сопоставлять между собой можно только однородные величины (имеющие один и тот же смысл и одинаковую размерность) и лишь в сходственных точках пространства и в сходственные моменты времени, т.е. отвечающие условиям
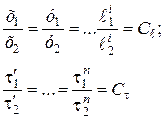
4. Подобие двух физических явлений означает подобие всех физических величин, характеризующих рассматриваемое явление. Это означает, что любая физическая переменная первого явления в сходственных точках пространства и в сходственные моменты времени пропорциональна однородной с ней величине второго явления, т.е.
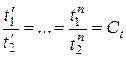 (температура);
(температура);
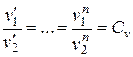 (скорость);
(скорость);
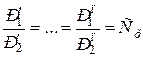 (давление).
(давление).
При этом в общем случае 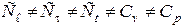 .
.
Большинство физических процессов, подлежащих изучению при разработке полезных ископаемых и при строительстве подземных сооружений, описывается условиями подобия, которые могут быть разделены на три группы: условия механического (силового) подобия, гидромеханического подобия и теплового подобия.
Условия механического подобия. Из второго закона механики Ньютона для двух явлений имеет место
| P1 = m1a1; P2 = m2a2. | (2.36) |
Приведем эти уравнения с помощью масштабных преобразований к безразмерному виду. После подстановки
| р1 = р1,0Р1; р2 = р2,0Р2; m1 = m1.0M1; m2 = m2.0M2; a1 = a1.0A1; a2 = a2.0A2, | (2.37) |
и соответствующих преобразований получим
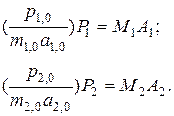
| (2.38) |
Очевидно, уравнения (2.38) будут тождественно одинаковыми в том случае, если коэффициенты в скобках будут равны между собой
или 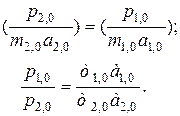 (2.39)
(2.39)
Откуда
Ср = СтСа (2.40)
Если массу выразить через объем и плотность, а ускорение через линейные размеры и время, то получим
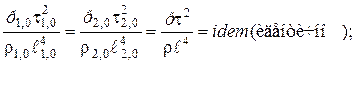 (2.41)
(2.41)
или 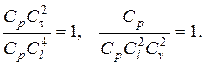 (2.42)
(2.42)
Следовательно, для обеспечения условий механического подобия должно соблюдаться уравнение связей (2.42) между множителями подобия.
Условие гидромеханического подобия (случай несжимаемой вязкой жидкости).
Предполагаем, что процессы движения жидкости происходят в геометрически подобных системах, т.е. должно соблюдаться условие (2.1).
Законы, описывающие движение жидкости.
Уравнение сплошности для двух систем
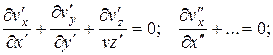 (2.43)
(2.43)
Соответственно, уравнения движения жидкости, в частности в направлении х
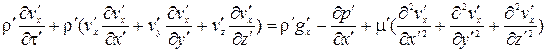
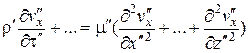 (2.44)
(2.44)
| где | vx, vy, vz | – | проекции скорости на оси; |
| r | – | плотность жидкости; | |
| gx | – | проекции ускорения силы тяжести на оси; | |
| р | – | удельное давление жидкости; | |
| m | – | коэффициент вязкости жидкости. |
Учитывая большую громоздкость формул, приведение их к безразмерному виду сделаем иначе, не прибегая к масштабным преобразованиям. Так как устанавливаются условия, обеспечивающие подобие процессов, то допустим, что процессы, протекающие в двух системах, подобны, и для этого определим, какие требования должны быть выполнены. Для подобных систем должно быть справедливо
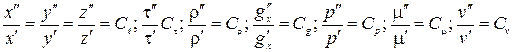
| (2.45) |
На основании этого все переменные второй системы могут быть выражены через переменные первой, а именно
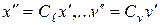 и т.д. (2.46)
и т.д. (2.46)
Подставив (2.46) в (2.43) и (2.44) получим для второй системы
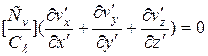 ; (2.47)
; (2.47)
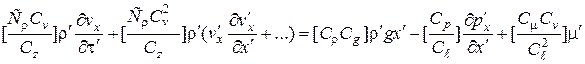 . (2.48)
. (2.48)
Очевидно, уравнения (2.43) и (2.44) будут подобны в том случае, если коэффициенты, состоящие из множителей подобия, могут быть сокращены и для этого они должны представлять собой:
из уравнения (2.47) следует
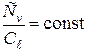 , (2.49)
, (2.49)
а из уравнения (2.48):
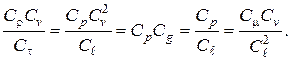 (2.50)
(2.50)
Таким образом, получены уравнения связи между множителями подобия. Следовательно, произвольно выбирать масштабы моделирования отдельных параметров нельзя, т.к. они связаны между собой зависимостями (2.49) и (2.30).
Рассматривая члены соотношения (2.50) попарно, имеем
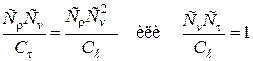
| (2.51) |
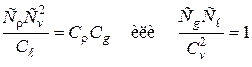
| (2.52) |
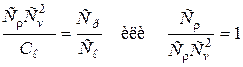
| (2.53) |
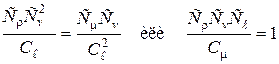
|
 (2.54) (2.54)
|
Условия (2.51)-(2.54) можно представить в виде критериев подобия. Для этого подставим вместо констант подобия их значения из уравнений (2.45) и сгруппировав все величины по индексам, получим
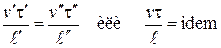 = Н0 (критерий гомохронности) (2.55)
= Н0 (критерий гомохронности) (2.55)
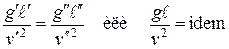 =Fr (критерий Фруда) (2.56)
=Fr (критерий Фруда) (2.56)
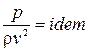 = Еu (критерий Эйлера) (2.57)
= Еu (критерий Эйлера) (2.57)
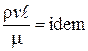 = Re (критерий Рейнольдса) (2.58)
= Re (критерий Рейнольдса) (2.58)
Следовательно, чтобы получить гидромеханическое подобие систем, необходимо для любых сходственных точек иметь одни и те же значения подобия Н0 , Fr , Еu , Re.
Одновременное соблюдение условий (2.55)-(2.58) встречает на практике большие затруднения или просто невозможно. В связи с этим при моделировании стремятся выполнить условия наиболее существенных, определяющих критериев подобия, которые устанавливаются в зависимости от типа изученной задачи и целей исследования. Так, при исследовании движения воды в пористых средах при очень малых числах Рейнольдса, т.е. в области линейной зависимости осредненной фильтрации от градиента давления, критерии Рейнольдса и Фруда не определяют движения, и при моделировании фильтрации должны быть выполнены иные специфические условия подобия. Опытами по моделированию интерференции скважин при водонапорном режиме установлено, что в области линейного закона фильтрации для однородной жидкости осуществляется потенциальное течение. Это обосновывает возможность широкого применения в конкретных гидромеханических расчетах при проектировании разработки нефтяных месторождений электрических аналогий (метод ЭГДА).
Приближенное подобие при моделировании физических процессов применяют также в случаях, если известны не все определяющие параметры изучаемого процесса или среди определяющих параметров имеются такие, влияние на процесс которых наиболее значительно по сравнению с другими, а также, если при наличии переменных параметров или анизотропии невозможно обеспечить условия подобия.
В указанных случаях моделирования используют те параметры, которые известны, или исключают из рассмотрения параметры, влияние которых незначительно. Степень приближения в каждом конкретном случае моделирования устанавливают на основании результатов исследований модели.
При решении конкретных задач к дифференциальным уравнениям (2.43), (2.44) и критериям подобия (2.55)-(2.58) необходимо присовокупить частные особенности, характеризующие свойство среды, ее форму и размеры, особенности протекания процесса на ее границах и т.д., которые однозначно выделяют рассматриваемый процесс из целого класса однородных процессов.
Условие теплового подобия. Тепловое подобие процессов означает подобие температурных полей и тепловых потоков в геометрически и гидромеханически подобных системах.
Пусть имеем две подобные между собой системы, тепловые процессы в которых описываются следующими уравнениями.
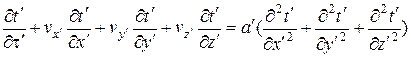 ; ;
| (2.59) |
 . .
| (2.60) |
Уравнение теплообмена (из законов Ньютона и Фурье)
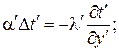 (2.61)
(2.61)
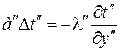 , (2.62)
, (2.62)
| где | 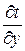
| – | нормальная производная к оси х |
| t | – | температура тела (жидкости); | |
| vx, vy vz | – | проекции скорости на оси x, y, z; | |
| а | – | коэффициент температуропроводности; | |
| α | – | коэффициент теплоотдачи; | |
| λ | – | коэффициент теплопроводности. |
Допустим, что системы подобны, т.е.
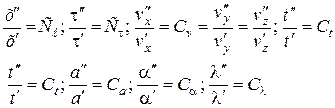
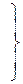 . (2.63)
. (2.63)
Заменяя переменные второй системы (2.60) и (2.62) через переменные первой, получим
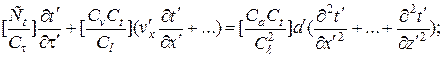 (2.64)
(2.64)
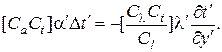 (2.65)
(2.65)
Из условия тождественности уравнения (2.59), (2.60) и (2.64), (2.65) имеем
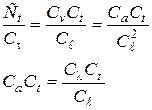
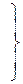 (2.66)
(2.66)
Откуда
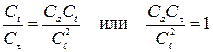 ; (2.67)
; (2.67)
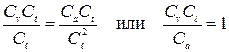 ; (2.68)
; (2.68)
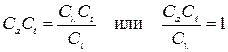 (2.69)
(2.69)
Подставив вместо констант подобия их значения из (2.63), получим критерии подобия
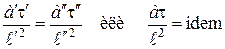 = F0 (критерий Фурье) (2.70)
= F0 (критерий Фурье) (2.70)
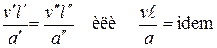 = Ре (критерий Пекле) (2.71)
= Ре (критерий Пекле) (2.71)
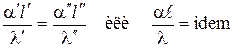 = Nu (критерий Нуссельта) (2.72)
= Nu (критерий Нуссельта) (2.72)
Таким образом, чтобы обеспечить тепловое подобие двух или нескольких систем, необходимо, чтобы в сходственных точках критерии подобия F0, Ре, Nu имели одни и те же значения. Здесь также необходимо отметить, что одновременное выполнения условий гидромеханического и теплового подобия невозможно. Поэтому в каждой конкретной задаче при моделировании должны соблюдаться только основные определяющие критерии подобия.
Дата добавления: 2017-10-04; просмотров: 3208;











