Методы фотомеханики
Впервые в горном деле оптико-поляризационный метод исследований был применен А.К. Зайцевым и Ф.Ю. Левинсон-Лесенгом для решения задачи о наиболее рациональной форме поперечного сечения тоннеля. Эксперименты проводились на пластинках из целлулоида с различными по форме отверстиями. Цель этих опытов – выяснить влияние отверстия и его формы на характер распределения напряжений под действием приложенной внешней нагрузки. Широкое применение для решения задач геомеханики получил этот метод в послевоенный период.
Оптико-поляризационный метод изучения НДС реализуется в виде методов фотомеханики, рассматривающих следующие свойства.
Фотоупругость – исследование процессов упругого деформирования материалов.
Фотопластичность – исследование процессов остаточного деформирования материалов при известных предшествующих состояниях.
Фотоползучесть – исследование поведения материалов во времени под нагрузкой.
Напряженное деформированное состояние исследуемых объектов зависит от характера внешних воздействий на них до и в момент проведения экспериментов. В задачах статическойфотомеханики физические воздействия, их интенсивность и направление остаются практически неизменными в течение достаточно длительного времени; силами инерции можно пренебречь.
В задачах динамическойфотомеханики, наоборот, учитывается изменение характеристик при механических воздействий во времени и влияние сил инерции.
В основе методов фотомеханики лежит эффект двойного лучепреломления, проявляющийся в оптически чувствительных материалах под воздействием механических напряжений. При просвечивании таких материалов поляризованным светом в моделях наблюдается оптическая картина, по которой судят о напряженно-деформированном состоянии моделируемого объекта.
Допустим, что в результате проведения горизонтальной выработки в массиве горных пород произойдет нарушение силового равновесия. Вокруг выработки возникает поле напряжений (рис.4.6, а), характер которого в случае однородных изотропных пород будет оставаться постоянным для любого поперечного сечения по длине выработки. Следовательно, задача может быть представлена как плоская для сечения, перпендикулярного оси выработки, которая имеет аналитическое решение.
Для изучения напряженного состояния пород вокруг выработки изготавливают модель из оптически активного материала с соблюдением условий геометрического и силового подобия. Через модель пропускают луч поляризованного света, и на экране получают поле напряжений (рис. 14, б) в виде линий

различных цветов и оттенков. На основании этого судят о качественной характеристике поля напряжений, о направлении векторов напряжений, о концентрации напряжений и о точках или районах, наиболее опасных с точки зрения устойчивости или прочности обнажения.
Методы фотомеханики позволяют применить и объемные модели. Так, например, при изучении оптическим методом прочности бурового инструмента и разрушаемости пород широко применяют объемные модели, на основании которых становится возможным составить тензор напряжений в контактных зонах, подойти к решению вопроса о роли ядра уплотнения в процессе воздействия бурового инструмента и о влиянии предварительных выколов и свободных поверхностей в процессе разрушения породы.
Кроме того, оптический метод позволяет оценить влияние параметров удара на разрушаемость горной породы и затупления лезвия бурового инструмента на эффективность бурения, а также помогает решить вопрос об участии волн напряжений в процессе разрушения горных пород при ударном бурении.
Методы объемной фотомеханики также применяют и для исследования статической работы подземных сооружений. В круг таких задач входит исследование напряженного состояния горного массива вокруг вертикальных и горизонтальных выработок, пройденных в слоистых породах с наклонным залеганием пластов и различными физико-механическими свойствами, исследование распределения напряжений в сопряжениях различных выработок, определение напряжений в крепях и массиве при переменном сечении выработок небольшой протяженности и т.д.
Наибольшее практическое значение имеют следующие типовые задачи механики горных пород:
I тип.Определение условий сохранения и потери устойчивости элементов массивов и сооружений при различных исходных состояниях и комплексах воздействий на них, в том числе при ведении горных работ. Элементами исследуемых объектов, устойчивость которых должна быть обеспечена, являются: поверхности подземных выработок (кровли, почвы, бока), целики, потолочные камеры и кровли лав, борты карьеров, земная поверхность. Учитывают стадийность процессов деформирования и разрушения элементов, предельные их состояния, а также видоизменения сочетаний условий.
II тип.Установлениезакономерностей взаимодействия элементов массивов между собой и с элементами сооружений, в том числе с крепями горных выработок, в зависимости от естественно-геологических условий и видов взаимодействий. Взаимодействием считается взаимозависимое изменение в пространстве и времени граничных поверхностей контакта. Вид закономерности механического взаимодействия крепи и пород, определяющий условия их совместной работы, реализуется в различных режимах, включая заданную нагрузку, заданную деформацию, взаимовлияющую деформацию, комбинированный режим.
III тип.Изучение влияния горных выработок и комплексов горных работ на окружающие породные массивы различных структур и свойств, находящиеся в различных состояниях и подвергающиеся различным воздействиям.
Основными вопросами изучения являются: установление зон опорного давления, разгрузки, сдвижений и разрушений массивов, определение очертаний и размеров защищенных зон, выяснение распространения волн напряжений, вызванных взрывами, на различные подземные и наземные объекты.
Таким образом, оптический метод исследования напряжений позволяет решать весьма сложные задачи, которые недоступны математическому анализу.
Теоретические основы оптического метода исследования упругих полей напряжений и смещений базируется на использовании закона Гука о прямой пропорциональности между напряжением и деформацией и на явлении оптической анизотропии изотропных тел, подвергнутых действию внешних сил, или при наличии внутренних напряжений. С помощью оптического метода обнаруживают не сами величины нормальных напряжений, а разность между ними, т.е. максимальные касательные напряжения 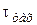
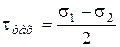 , (4.41)
, (4.41)
где 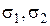 – главные нормальные напряжения.
– главные нормальные напряжения.
Поэтому с помощью оптического метода определяется существенная характеристика для суждения о прочности конструкции по теории Кулона.
Второй принцип, использованный при оптическом моделировании, вытекает из общей теории света. Если, например, световой луч от обычного источника света направить на стеклянную пластинку под углом, то луч делится на две части: одна часть – отражается, другая – преломляется. Опыты показывают, что отраженный и преломленный лучи оказывается плоско-поляризованными и их колебания будут происходить в двух взаимно перпендикулярных плоскостях.
Наибольшей поляризации световой луч достигает в том случае, если отраженный и преломленный лучи перпендикулярны друг другу (рис.4.7).


Интересными оптическими свойствами обладает ряд кристаллов (турмалин, слюда, кальций). Если кристалл кальцита поставить своим основанием на бумагу с черной точкой и посмотреть сверху, то можно увидеть два изображения точки (рис.4.8).
В этом случае имеет место двойное лучепреломление. Ели теперь с помощью пластинки турмалина проанализировать обыкновенный и необыкновенный лучи, то оказывается, что оба луча являются плоско-поляризованными.
При этом колебания обыкновенного луча происходят в плоскости, перпендикулярной диагональной плоскости 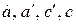 , а колебания необыкновенного луча лежат в этой плоскости
, а колебания необыкновенного луча лежат в этой плоскости 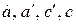 , т.е. колебания лучей происходят в двух взаимно перпендикулярных плоскостях.
, т.е. колебания лучей происходят в двух взаимно перпендикулярных плоскостях.
Явление двойного лучепреломления можно также наблюдать и в изотропных веществах под действием нагрузки. Например, сформированный или напряженный кусок стекла, целлулоида, акелита и т.д. обнаруживает все свойства двойного лучепреломления. Свойство двойного лучепреломления изотропных тел под нагрузкой (открыто Брюстером в 1816 г.) положило начало методу фотоупругости.
Как известно, при плоском напряженном состоянии тела в каждой точке имеются площадки, по которым касательные напряжения отсутствуют и действуют только главные нормальные напряжения 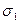 и
и 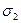 . Под действием этих напряжений создаются деформации, которые приводят материал к оптической анизотропии. Вследствие этого луч света, проходящий через напряженное прозрачное тело, будет разлагаться на два плоско-поляризованных луча, колебания которых лежат в двух взаимно перпендикулярных плоскостях, параллельных направлению распространения луча.
. Под действием этих напряжений создаются деформации, которые приводят материал к оптической анизотропии. Вследствие этого луч света, проходящий через напряженное прозрачное тело, будет разлагаться на два плоско-поляризованных луча, колебания которых лежат в двух взаимно перпендикулярных плоскостях, параллельных направлению распространения луча.
При этом распространение лучей в напряженно-деформированной пластине происходит с различными скоростями в соответствии с величинами 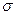 и
и 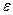 , что приводит к оптическому сдвигу фаз и линейной разности хода. Как показывают многочисленные опыты, разность хода в общем случае определяется по формуле
, что приводит к оптическому сдвигу фаз и линейной разности хода. Как показывают многочисленные опыты, разность хода в общем случае определяется по формуле
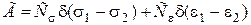 , (4.42)
, (4.42)
где 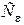 и
и 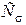 – постоянные, называемые оптическими коэффициентами деформации и напряжения, зависящими от применяемых материалов;
– постоянные, называемые оптическими коэффициентами деформации и напряжения, зависящими от применяемых материалов;
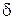 – толщина пластинки;
– толщина пластинки;
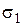 и
и 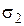 – главные нормальные напряжения;
– главные нормальные напряжения;
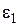 и
и 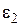 –деформации в направлении главных нормальных напряжений.
–деформации в направлении главных нормальных напряжений.
Поскольку в стадии упругого деформирования материалов существует строгая пропорциональность между 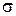 и
и 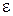 , обобщенная зависимость (4.42) преобразуется к виду
, обобщенная зависимость (4.42) преобразуется к виду
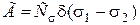 . (4.43)
. (4.43)
В этом случае выражение (4.42) согласно (4.43) можно представить в виде
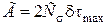 . (4.44)
. (4.44)
При пластичном деформировании материалов на интерферационную картину полос решающее влияние оказывают деформации, так как напряжения на этой стадии деформации изменяются незначительно. В связи с этим зависимость (4.44) может быть представлена в виде линий
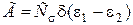 . (4.45)
. (4.45)
Следовательно, зная толщину модели 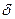 , оптическую постоянную
, оптическую постоянную 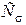 и определив разность хода
и определив разность хода 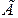 , можно установить значение максимальных скалывающих напряжений при исследовании модели в стадии упругого деформирования и относительных деформаций при изучении процессов ползучести или пластического деформирования.
, можно установить значение максимальных скалывающих напряжений при исследовании модели в стадии упругого деформирования и относительных деформаций при изучении процессов ползучести или пластического деформирования.
Определение разности хода 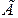 основывается на свойстве поляризованного света в зависимости от частоты колебаний давать различные цвета. Точно так же, как частота звукового колебания определяет высоту звука, частота светового колебания определяет качество света, которое глаз воспринимает как цвет.
основывается на свойстве поляризованного света в зависимости от частоты колебаний давать различные цвета. Точно так же, как частота звукового колебания определяет высоту звука, частота светового колебания определяет качество света, которое глаз воспринимает как цвет.
Следовательно, определенной частоте колебания соответствует определенный цвет. Луч света, составленный только из одного цвета, называется монохроматическим, или однородным.
Очевидно, для каждого монохроматического света имеется вполне определенная длина волны. Так как длина волны определяется выражением
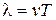 ,
,
где 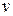 – скорость распространения света;
– скорость распространения света;
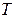 – период колебания волны,
– период колебания волны,
а частота колебания при этом определяется как величина, обратная периоду колебания:
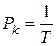 ,
,
то можно установить связь между частотой колебания и длиной волны, а, следовательно, и цветом света. В пустоте все лучи монохроматического света распространяются с одинаковой скоростью 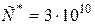 см/с.
см/с.
Следовательно, длина волны для каждого монохроматического света будет определяться только в зависимости от частоты колебания 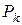 :
:
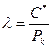 . (4.46)
. (4.46)
Поэтому, получив на экране различные цвета, можно определить, имея таблицу соотношений цвета и длины волн, величину разности хода 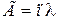 , а следовательно, пользуясь формулой (4.41), можно получить величину максимальных касательных напряжений
, а следовательно, пользуясь формулой (4.41), можно получить величину максимальных касательных напряжений
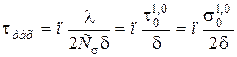 , (4.47)
, (4.47)
где 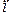 – порядок полосы;
– порядок полосы;
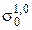 – цена полосы оптически чувствительного материала.
– цена полосы оптически чувствительного материала.
Разность хода может быть определена по методу сопоставления цветов, по методу полос и по методу компенсаций. При методе сопоставления цветов искомую разность хода определяют непосредственно по цветной картинке изохром, полученной при белом источнике света, и последующем сопоставлении с интерферационными цветами эталонных колец Ньютона, для которых составлена таблица. При методе полос используется монохроматический источник света и учитываются порядковый номер полосы в исследуемой области, а также цена полосы материала. При методе компенсаций к искомой разности хода, создаваемой в упругой напряженной области объекта, оператор добавляет компенсатором разность хода, равную по величине, но обратную по знаку. При результирующей разности хода, равной нулю, при скрещенных поляроидах в измеряемой точке модели наблюдается затемнение.
После этих замечаний можно приступить к рассмотрению принципа действия оптико-поляризационной установки.
Рассмотрим образец изотропного прозрачного тела, подвергнутого рав-
номерной нагрузке (рис.4.9).

Обыкновенный луч, проходя через поляризатор 1, приобретает только вертикальные колебания и падает на образец 2, повернутый на угол 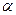 к горизонтальной оси. В результате напряженного состояния образца поляризованный свет, преломляясь, распадается на два луча. Колебания лучей идут в плоскостях главных напряжений. В результате преломления в зависимости от напряженности образца лучи приобретают разные скорости распространения. Пройдя образец, лучи падают на анализатор 3, ориентированный так, что он пропускает только колебания, перпендикулярные плоскости поляризации поляризатора 1. Таким образом, через анализатор пройдут только лучи
к горизонтальной оси. В результате напряженного состояния образца поляризованный свет, преломляясь, распадается на два луча. Колебания лучей идут в плоскостях главных напряжений. В результате преломления в зависимости от напряженности образца лучи приобретают разные скорости распространения. Пройдя образец, лучи падают на анализатор 3, ориентированный так, что он пропускает только колебания, перпендикулярные плоскости поляризации поляризатора 1. Таким образом, через анализатор пройдут только лучи 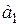 и
и 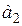 . Так как после образца лучи вследствие разной скорости распространения получили некоторую разность хода, то следовательно и после анализатора получили некоторую разность хода между горизонтальными составляющими колебаний.
. Так как после образца лучи вследствие разной скорости распространения получили некоторую разность хода, то следовательно и после анализатора получили некоторую разность хода между горизонтальными составляющими колебаний.
Если обозначить через 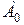 амплитуду колебаний луча после поляризатора:
амплитуду колебаний луча после поляризатора: 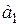 и
и 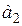 – амплитуды колебаний лучей после анализатора, то можно написать следующую зависимость для результирующей амплитуды колебаний после анализатора:
– амплитуды колебаний лучей после анализатора, то можно написать следующую зависимость для результирующей амплитуды колебаний после анализатора:
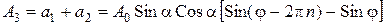 .
.
Значение 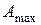 достигается при
достигается при 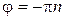
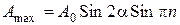 .
.
Интенсивность света
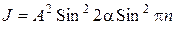 .
.
Максимальная интенсивность света имеет место при 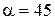 о, давая наиболее яркую картину цветов на экране, а следовательно, распределения, скалывающие напряжения
о, давая наиболее яркую картину цветов на экране, а следовательно, распределения, скалывающие напряжения 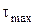 . Кроме ярких цветов на экране получают и темные места, которые удовлетворяют одному из трех условий:
. Кроме ярких цветов на экране получают и темные места, которые удовлетворяют одному из трех условий:
1. Свободные от напряжения точки, не дающие двух преломлений (поляризатор и анализатор скрещены, свет будет в них погашен).
2. Точки, в которых главные напряжения равны. В этих точках нет сдвига фаз, как нет и разности хода (скорости распространения лучей равны друг другу). Следовательно, амплитуды 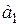 и
и 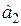 при этом равны и тогда имеем
при этом равны и тогда имеем
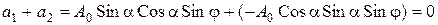 .
.
Это дает в результате темноту на экране. Наличие таких особых точек является весьма значительным при изучении моделей, так как в них 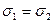 .
.
3. Точки, для которых плоскости направления главных напряжений совпадают с плоскостями поляризатора и анализатора. В этом случае 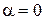 при 90 о и
при 90 о и 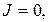 т.к.
т.к. 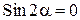 .
.
Последний случай представляет большую ценность для исследования напряжений, т.к. он дает точные сведения о направлении двух главных напряжений в любой точке образца. Следовательно, вращая образец (или поляризатор – анализатор) с одновременным отсчетом углов, для каждого угла получим систему черных точек для линий, в которые эти точки могут сливаться. В этих точках будем знать направления главных напряжений. Линии, соединяющие точки, где направления главных напряжений совпадают с плоскостями поляризации поляризатора и анализатора, называются изоклинами. Допустим, имеем изоклину 1, соответствующую углу поворота образца на угол 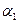 , изоклину 2,
, изоклину 2,
соответствующую углу поворота образца на угол 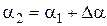 и т.д. (рис.4.10).
и т.д. (рис.4.10).
 Проведем из точек
Проведем из точек 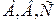 прямые под углами к вертикали, равными соответственно
прямые под углами к вертикали, равными соответственно 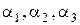 и т.д. Точки пересечения прямых между собой обозначим через
и т.д. Точки пересечения прямых между собой обозначим через 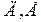 . Получим, таким образом, ломаные линии, которые являются изостатами (кривые направления одной из главных сил напряжения
. Получим, таким образом, ломаные линии, которые являются изостатами (кривые направления одной из главных сил напряжения 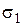 ). В каждой точке изостаты под углом 90 о к изолинии
). В каждой точке изостаты под углом 90 о к изолинии 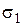 направлена
направлена 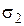 . Таким образом, изостаты представляют собой ортогональное семейство кривых, касательные к которым совпадают с направлением главных нормальных напряжений.
. Таким образом, изостаты представляют собой ортогональное семейство кривых, касательные к которым совпадают с направлением главных нормальных напряжений.
Чтобы отличить темные места, соответствующие изоклинам, от тех, которые являются следствием условий 1 и 2, надо помнить, что изоклины изменяют свое положение при последовательных поворотах образца или системы поляризатора-анализатора. Точки образца, где 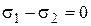 (т.е. свободные от напряжения), при любом повороте остаются на тех же местах.
(т.е. свободные от напряжения), при любом повороте остаются на тех же местах.
Таким образом, при исследовании образца или модели на изолированной установке получают значение 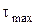 , после напряжений
, после напряжений 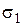 и
и 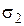 , а, следовательно, определяют область пониженных и повышенных напряжений.
, а, следовательно, определяют область пониженных и повышенных напряжений.
Изучение напряжений на объемных моделях основано на методе «замораживания» напряжений (деформаций) и методе рассеянного света. Первый метод, в котором предусматривается использование обычных поляризационных установок, нашел более широкое применение. Второй требует специального оптического оборудования, промышленное изготовление которого еще не налажено.
При методе рассеянного света нагруженная модель помещается в иммерсионную жидкость и просвечивается тонкой полоской плоско-поляризованного монохроматического света большой яркости, который проходя через модель, освещает рассматриваемую плоскость внутри модели. В просвечиваемом сечении при наблюдении со стороны, перпендикулярной к плоскости сечения, видна картина полос интерференции света, связанных с коэффициентом преломления, а следовательно, и с деформацией в каждой точке модели.
Разность квазиглавных нормальных напряжений, лежащих в плоскости, перпендикулярной к проходящему лучу, определится по формуле
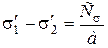 , (4.48)
, (4.48)
где 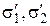 – квазиглавные напряжения (наибольшие и наименьшие нормальные напряжения в исследуемой плоскости);
– квазиглавные напряжения (наибольшие и наименьшие нормальные напряжения в исследуемой плоскости);
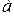 – расстояние между полосами интерференции;
– расстояние между полосами интерференции;
Направляя плоский пучок поляризованного света различным образом по отношению к модели, можно определить напряжение в любом сечении модели без предварительного приготовления специальных срезов, как это делается при методе «замораживания».
Метод «замораживания» основан на способности некоторых оптически активных материалов, нагруженных при нагреве и охлажденных под нагрузкой до комнатной температуры, сохранять оптический эффект после снятия нагрузки. Модели изготавливают из оптически активных материалов, имеющих двухфазную структуру. При нагревании модели из таких материалов до определенных температур, в зависимости от вида и марки материала, большая часть материала размягчается и не оказывает сопротивления прилагаемой нагрузке. Часть материала (скелет), оставшаяся в твердом состоянии, полностью воспринимает прилагаемую нагрузку, под действием которой в модели возникают деформации и напряжения. Если затем, не снимая нагрузки, модель охладить до комнатной температуры, то размягченная при нагревании часть материала затвердевает (замораживается) и будет удерживать полученную скелетом деформацию при снятии нагрузки, а также и после распиливания модели в различных направлениях на тонкие пластинки толщиной 2…4 мм. В дальнейшем, через каждую такую пластинку, представляющую уже плоскую модель, пропускается луч поляризованного света, и на экране получается плоское поле напряжений. В результате на основании просвечивания поляризованным светом всех пластинок получим объемную картину распределения напряжений в модели, соответствующую характеру распределения напряжений в натуре.
Оптический эффект, получающийся при прохождении поляризованного света через объемную модель, связан с понятием квазиглавных напряжений 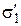 и
и 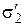 . При нормальном просвечивании среза (пластинки) квазиглавные напряжения
. При нормальном просвечивании среза (пластинки) квазиглавные напряжения 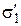 и
и 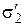 действуют так же, как главные напряжения
действуют так же, как главные напряжения 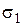 и
и 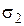 в плоской модели.
в плоской модели.
Квазиглавные напряжения могут быть выражены через неглавные напряжения, действующие в той же плоскости, аналогично плоской задаче. Например, для плоскости 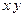 , нормальной к оси
, нормальной к оси 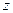 , напряжения
, напряжения 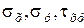 , отнесенные к осям
, отнесенные к осям 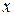 и
и 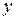 , связаны с разностью квазиглавных напряжений соотношениями:
, связаны с разностью квазиглавных напряжений соотношениями:
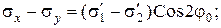 (4.49)
(4.49)
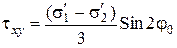 , (4.50)
, (4.50)
где 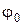 – угол между направлением
– угол между направлением 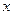 и направлением квазиглавного напряжения
и направлением квазиглавного напряжения 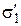 .
.
Поляризованный луч света, пройдя пластинку с «замороженными» напряжениями, приобретает некоторую разность хода 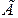 , пропорциональную разности квазиглавных напряжений (
, пропорциональную разности квазиглавных напряжений ( 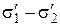 ), лежащих в плоскости, перпендикулярной к оси распространения света:
), лежащих в плоскости, перпендикулярной к оси распространения света:
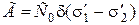 , (4.51)
, (4.51)
или выражая разность хода через число полос, получаем
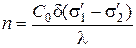 , (4.52)
, (4.52)
где 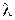 – длина волны применяемого света;
– длина волны применяемого света;
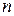 – число полос.
– число полос.
Таким образом, полученные из объемной модели, исследуют аналогично
плоской модели.
Подобие при оптическом методе. При изучении оптических явлений с
помощью оптического метода необходимо так же, как при других методах моделирования физических явлений, соблюдать подобие соответственных одноименных параметров и комплексов. Установление связей между константами подобия и выявление критериев подобия находят из анализа размерностей самых общих уравнений, описывающих изучаемое явление. Поэтому в зависимости от постановки задачи: изучается ли процесс резания, удара или статического давления, для каждого процесса должны быть установлены значения критериев и множителей подобия.
Например, при моделировании задач в стадии упругого деформирования, связанных с установлением общей картины напряженно-деформированного состояния массива горных пород при разработке месторождений полезных ископаемых, необходимо обеспечить условия подобия и применять для перехода от модели к натуре исходя из зависимостей, приведенных в табл. 4.1.
Таблица 4.1
| Действующие нагрузки | Условия подобия | ||
| смещения | деформации | напряжения | |
| Объемные силы тяжести | 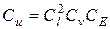
| 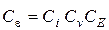
| 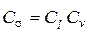
|
| Объемные центробежные силы | 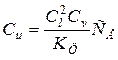
| 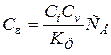
| 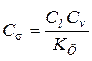
|
| Распределенная нагрузка по площади |
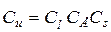
|
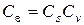
|
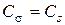
|
| Распределенная нагрузка по длине |
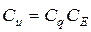
| 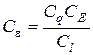
| 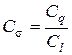
|
| Сосредоточенные силы | 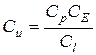
| 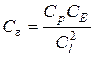
| 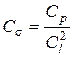
|
Примечание. 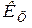 – масштаб центрифугирования; – масштаб центрифугирования; 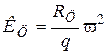 , ,
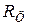 – радиус вращения; – радиус вращения; 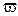 – угловая скорость; – угловая скорость;
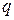 – ускорение силы тяжести. – ускорение силы тяжести.
|
Временное условие подобия определяется исходя из выражения
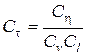 , (4.53)
, (4.53)
где 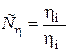 – множитель подобия вязкости.
– множитель подобия вязкости.
Выполнение граничных условий достигается при равенстве коэффициентов бокового распора:
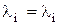 . (4.54)
. (4.54)
Дата добавления: 2017-10-04; просмотров: 1628;











