V. ЛОГИЧЕСКИЕ ОСНОВЫ ВЫЧИСЛИТЕЛЬНОЙТЕХНИКИ
ПОНЯТИЕ О ЛОГИЧЕСКОЙ ФУНКЦИИ И ЛОГИЧЕСКОМ УСТРОЙСТВЕ
Для обозначения различных предметов, понятий, действий пользуются словами. Слова строятся из букв, которые берутся из некоторого их набора, называемого алфавитом.
В цифровой технике для тех же целей пользуются кодовыми словами. Особенность этих слов состоит в том, что все они имеют одинаковую длину (т. е. представляют собой последовательность букв одинаковой длины) и для их построения используется простейший алфавит, состоящий лишь из двух букв. Эти буквы принято обозначать символами 0 и 1. Таким образом, кодовое слово в цифровой технике есть последовательность символов 0 и 1 определенной длины, например 10111011. Такими словами могут представляться и числа, в этом случае 0 и 1 совпадают по смыслу с обычными арабскими цифрами. При представлении кодовым словом некоторой нечисловой информации, чтобы отличать буквы 0 и 1 от цифр, будем эти буквы называть соответственно логическим нулем и логической единицей.
Если длина кодовых слов составляет n разрядов, то можно построить 2n различных комбинаций — кодовых слов. Например, при n=3 можно построить 23 = 8 слов: 000, 001, 010, O11, 100, 101, 110, 111.
Информация, которая передается между отдельными узлами (блоками) сложного цифрового устройства, представляется в виде кодовых слов. Таким образом, на входы каждого узла поступают кодовые слова, на выходе узла образуется новое кодовое слово, представляющее собой результат обработки входных слов. Выходное слово зависит от того, какие слова поступают на входы узла. Поэтому можно говорить, что выходное слово есть функция, для которой аргументами являются входные слова. Для того чтобы подчеркнуть особенность таких функций, состоящую в том, что сама функция и ее аргументы могут принимать значения лог. 0 и лог. 1, будем эти функции называть функциями алгебры логики (ФАЛ).
Устройства, предназначенные для формирования функций алгебры логики, в дальнейшем будем называть логическими устройствами или цифровыми устройствами.
Цифровые устройства (либо их узлы) можно делить на типы по различным признакам.
По способу ввода и вывода кодовых слов различают логические устройства последовательного, параллельного и смешанного действия.
На входы устройства последовательного действия символы кодовых слов поступают не одновременно, а последовательно, символ за символом (в так называемой последовательной форме). В такой же последовательной форме выдается выходное слово.
На входы устройства параллельного действия все n символов каждого входного кодового слова подаются одновременно (в так называемой параллельной форме). В такой же форме образуется на выходе выходное слово. Очевидно, при параллельной форме приема и выдачи кодовых слов в устройстве необходимо иметь для каждого разряда входного (выходного) слова отдельный вход (выход).
В устройствах смешанного действия входные и выходные кодовые слова представляются в разных формах. Например, входные слова — в последовательной форме, выходные — в параллельной. Устройства смешанного действия могут использоваться для преобразования кодовых слов из одной формы представления в другую (из последовательной формы в параллельную или наоборот).
По способу функционирования логические устройства (иихсхемы) делят на два класса: комбинационные устройства (и соответственно комбинационные схемы) и последовательностные устройства (последовательностные схемы).
В комбинационном устройстве (называемом также автоматом без памяти) каждый символ на выходе (лог. 0 или лог. 1) определяется лишь символами (лог. 0 или лог. 1.), действующими в данный момент времени на входах устройства, и не зависит от того, какие символы ранее действовали на этих входах, В этом смысле комбинационные устройства лишены памяти (они не хранят сведений о прошлом работы устройства).
В последовательностных устройствах (или автоматах с памятью) выходной сигнал определяется не только набором символов, действующих на входах в данный момент времени, но и внутренним состоянием устройства, а последнее зависит от того, какие наборы символов действовали во все предшествующие моменты времени. Поэтому можно говорить, что последовательностные устройства обладают памятью (они хранят сведения о прошлом работы устройства).
Рассмотрим примеры комбинационного и последовательностного устройств.
Пусть устройство предназначено для формирования на выходе сигнала, определяющего совпадение сигналов на входах: на выходе формируется лог. 1 в случаях, когда на обоих входах действует лог. 1 либо на обоих входах действует лог. 0; если на одном из входов действует лог. 1, а на другом—лог. 0, то на выходе устройства образуется лог. 0. Такое устройство является комбинационным, в котором значение формируемой на выходе логической функции определяется лишь значениями ее аргументов в данный момент времени.
Рассмотрим другой пример. Счетчик подсчитывает импульсы. В каждый момент времени его состояние соответствует числу поступивших на вход импульсов. Выходная информация определяется тем, каково было состояние счетчика до данного интервала времени и поступает или нет на вход импульс в этом интервале времени. Таким образом, данное устройство является последовательностным устройством.
ЭЛЕМЕНТАРНЫЕ ЛОГИЧЕСКИЕ ФУНКЦИИ
В классической математике для задания функции обычно используются два способа: аналитический (запись формулой) и табличный (таблицами значений функции, какие приводятся, например, в справочниках). Подобными же способами могут задаваться логические функции.
При использовании табличного способа задания логических функций строится так называемая таблица истинности, в которой приводятся все возможные сочетания значений аргументов и соответствующие им значения логической функции. Так как число таких сочетаний конечно, таблица истинности позволяет определять значение функции для любых значений аргументов (в отличие от таблиц математических функций, которые позволяют задавать значения функции не для всех, а лишь для некоторых значений аргументов).
Таблица истинности функций двух аргументов представлена в табл. 1. Существует всего четыре функции одного аргумента.
Таблица 1.
| Аргумент x | Функция | |||
| f1(x) | f2(x) | f3 (x) | f4 (x) | |
Если число аргументов функции равно n, то число различных сочетаний (наборов) значений аргументов составляет 2n, а число различных функций п аргументов—22n. Так, при n=2 число наборов значений аргументов равно 22=4, число функций 24=16. Таблица истинности логических функций двух аргументов представлена в табл. 2.
Таблица 2.
| Аргу- менты | Функция | ||||||||||||||||
| x1 | x2 | f0 | f1 | f2 | f3 | f4 | f5 | f6 | f7 | f8 | f9 | f10 | f11 | f12 | f13 | f14 | f15 |
Возможен и аналитический способ записи логической функции. В обычной математике аналитический способ представления функции предполагает запись функции в виде математического выражения, в котором аргументы функции связываются определенными математическими операциями. Подобно этому аналитический способ задания логической функции предусматривает запись функции в форме логического выражения, показывающего, какие и в какой последовательности должны выполняться логические операции над аргументами функции.
Функции одного аргумента (табл. 1) представляются следующими выражениями:
f1(x) = 0 (константа 0); f2(x)=x;

f3(х) = f4(х) = 1 (константа 1).
Устройства, реализующие функции f1(x), f2(x) и f4(x), оказываются тривиальными. Таким образом, из всех функций одного аргумента практический интерес может представлять лишь функция f3(х), которую называют инверсией или логическое НЕ.
Из таблиц истинности функций f0 – f15 (табл. 2) наиболее широко используемыми являются:
f1(x1,x2) = x1*x1 – конъюнкции, логическое произведение, И;
f7(x1,x2) = x1 + x2 – дизъюнкции, логическое сложение, ИЛИ;

f14(x1,x2) = – логическое ИЛИ-НЕ;

f14(x1,x2) = – логическое И-НЕ.
Остальные из приведенных в табл. 2 функций либо не используются, либо используются редко.
В дальнейшем функции одного и двух аргументов будем называть элементарными логическими функциями, имея в виду, что логические выражения этих функций, содержащие не более одной логической операции, элементарны.
Свойства конъюнкции, дизъюнкции и инверсии.
Конъюнкция переменных х1 и х2 равна лог. 1 в том случае, когда и x1 и x2 равны лог. 1 (отсюда возникло название операции логическое И).
Дизъюнкция переменных х1 и x2 равна лог. 1, если или х1 или x2 равны лог. 1 (отсюда понятно возникновение названия операции логическое ИЛИ).
В тех случаях, когда число переменных больше двух, конъюнкция их равна лог. 1 при равенстве лог. 1 всех переменных; дизъюнкция равняется лог. 1, если хотя бы одна из них равна лог. 1.
В математике установлен определенный порядок выполнения операций в сложном выражении. Например, вначале выполняется операция умножения и затем операция сложения. Если требуется изменить этот порядок, используются скобки.
Подобно этому и для сложного логического выражения установлен определенный порядок выполнения операций: вначале выполняются операции инверсии, затем операции конъюнкции и в последнюю очередь операции дизъюнкции. Например, запись логического выражения х1+х2*x3+x4*x2 предполагает, что при вычислении выражения

вначале выполняется операция инверсии х3, затем операции конъюнкции и в последнюю очередь — операции дизъюнкции. А если требуется нарушить это правило, используются скобки. В этом случае вначале выполняются операции в скобках (а если одни скобки вложены в другие, то вначале выполняются операции в самых внутренних скобках).
Операции конъюнкции и дизъюнкции обладают рядом свойств:
сочетательный закон : x1*(x2*x3) = (x1*x2)*x3
x1+(x2+x3) = (x1+x2)+x3;
переместительный закон: x1*x2 = x2*x1
x1+x2 = x2+x1;
распределительный закон: x1+(x2*x3) = (x1+x2) * (x1+x3).
Легко убедиться в справедливости следующих выражений:
1*х=х; х*х=х; 1+x=1; х+х=х;


0*х=0; ; 0+х=х; .
Кроме того, существуют так называемые формулы де Моргана:

Можно сформулировать следующее правило применения формул де Моргана к сложным логическим выражениям. Инверсия любого сложного выражения, в котором аргументы (либо их инверсии) связаны операциями конъюнкции и дизъюнкции, может быть представлена тем же выражением без инверсии с изменением всех знаков конъюнкции на знаки дизъюнкции, знаков дизъюнкции на знаки конъюнкции и инверсией всех аргументов.
ПОЛНЫЕ СИСТЕМЫ ФУНКЦИИ АЛГЕБРЫ ЛОГИКИ.
Очевидно, могут быть построены простейшие логические элементы, реализующие элементарные логические функции двух переменных f0,..., f15. Сложные логические функции могут быть построены последовательным выполнением функциональных зависимостей, связывающих пары переменных.
Следовательно, имея элементы, осуществляющие элементарные операции f0,..., f15 можно выполнить любую сложную логическую операцию. Такую систему функций можно назвать полной системой, или базисом. Условие наличия 16 различных типов логических элементов, каждый из которых реализует одну из 16 элементарных функций /о,..., /is, является достаточным для синтеза логического устройства любой сложности, но оно не является необходимым, т. е. при синтезе можно ограничиться меньшим набором элементарных функций, взятыхf0,..., f15.
Последовательно исключая из базиса функции, можно получить так называемый минимальный базис. Под минимальным базисом понимают такой набор функций, исключение, из которого любой функции превращает полную систему функций в неполную.
Возможны различные базисы и минимальные базисы, отличающиеся друг от друга числом входящих в них функций и видом этих функций. Выбор того или иного базиса для синтеза логических устройств связан с тем, насколько просто, удобно и экономично технически выполнить элементы, реализующие входящие в базис функции, и в целом все логическое устройство.
Как показано выше, с помощью логических операций конъюнкции (И), дизъюнкции (ИЛИ) и инверсии (НЕ) можно выразить любую другую из элементарных функций f0,..., f15. Следовательно, эта совокупность логических функций образует базис. Это означает, что любая логическая функция, как бы сложна она ни была, может быть представлена через логические операции И, ИЛИ, НЕ. Иначе, можно построить любое логическое устройство, имея лишь три типа логических элементов, выполняющих операции И, ИЛИ,НЕ.
Однако, базис И, ИЛИ, НЕ не является минимальным. Из этой совокупности функций можно исключить функцию И либо функцию ИЛИ и оставшийся набор функций будет удовлетворять свойствам базиса. Действительно, если исключить функцию И, то операцию И можно выразить через оставшиеся операции ИЛИ и НЕ. Чтобы показать это, нужно дважды проинвертировать конъюнкцию и применить затем правило де Моргана.
Хотя операцию И и можно выразить через операции ИЛИ и НЕ, но это сложно (требуется выполнение трех операций инверсии и одной операции ИЛИ), поэтому на практике используется неминимальный базис, включающий в себя все три функции И, ИЛИ, НЕ.
В настоящее время базис И, ИЛИ, НЕ обычно используется при начальной стадии проектирования устройств для построения функциональной схемы. Для реализации устройств обычно используются базисы И-НЕ либо ИЛИ-НЕ. Элементы этого базиса широко выпускаются промышленностью в интегральном исполнении.
ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ ОБЩИЕ СВЕДЕНИЯ.
Выше отмечалось, что логические функции и их аргументы принимают значение лог. 0 и лог. 1. При этом следует иметь в виду, что в устройствах лог. 0 и лог. 1 соответствует напряжение определенного уровня (либо формы). Наиболее часто используется два способа физического представления лог. 0 и лог. 1: потенциальный и импульсный.
При потенциальной форме для представления лог. 0 и лог. 1 используется напряжение двух уровней: высокий уровень соответствует лог. 1 (уровень лог. 1) и низкий уровень соответствует лог. 0 (уровень лог. 0). Такой способ представления значений логических величин называется положительной логикой. Относительно редко используют так называемую отрицательную логику, при которой лог. 1 ставят в соответствии низкий уровень напряжения, а лог. 0 — высокий уровень. В дальнейшем, если это не оговаривается особо, будем пользоваться только положительной логикой.
При импульсной форме лог. 1 соответствует наличие импульса, логическому 0 — отсутствие импульса.
Заметим, что, если при потенциальной форме соответствующая сигналу информация (лог. 1 либо лог. 0) может быть определена практически в любой момент времени, то при импульсной форме соответствие между уровнем напряжения и значением логической величины устанавливается в определенные дискретные моменты времени (так называемые тактовые моменты времени).
ОСНОВНЫЕ ПАРАМЕТРЫ ИНТЕГРАЛЬНЫХ ЛОГИЧЕСКИХ ЭЛЕМЕНТОВ.
Рассмотрим основные параметры логических элементов и методы их улучшения.
Коэффициент объединения по входу определяет число входов элемента, предназначенных для подачи логических переменных. Элемент с большим коэффициентом объединения по входу имеет более широкие логические возможности.
Нагрузочная способность (или коэффициент разветвления по выходу) определяет число входов аналогичных элементов, которое может быть подключено к выходу данного элемента. Чем выше нагрузочная способность элементов, тем меньшее число элементов может потребоваться при построении цифрового устройства.
Для повышения нагрузочной способности в элементах применяют усложненную схему инвертирующей части. Повышение нагрузочной способности элемента связано с тем, что выходной транзистор, через который замыкается ток нагрузки, удерживается в открытом состоянии большим базовым током, который обеспечивается эмиттерной цепью транзистора.
В выключенном состоянии элемента с простым инвертором ток в нагрузку, подается от источника питания через коллекторный резистор с большим сопротивлением. Этот резистор ограничивает максимальное значение тока в нагрузке (с ростом тока нагрузки увеличивается падение напряжения на Rк, уменьшается напряжение на выходе). В элементе со сложным инвертором в нагрузку подается эмиттерный ток транзистора , работающего в схеме эмиттерного повторителя. Так как выходное сопротивление эмиттерного повторителя мало, то выходное напряжение слабее зависит от тока нагрузки и допустимы большие значения нагрузочного тока.
Быстродействие логических элементов является одним из важнейших параметров логических элементов, оно оценивается задержкой распространения сигнала от входа к выходу элемента.
Рассмотрим факторы, влияющие на быстродействие логического элемента, и методы повышения быстродействия.
Для повышения скорости переключения транзисторов в элементе необходимо использовать более высокочастотные транзисторы и переключение транзисторов производить большими управляющими токами в цепи базы; существенное уменьшение времени задержки достигается благодаря использованию ненасыщенного режима работы транзисторов (в этом случае исключается время, необходимое на рассасывание неосновных носителей в базе при выключении транзисторов).
Задержка распространения сигнала связана также с необходимостью перезарядки емкости нагрузки и паразитных монтажных емкостей. Этот процесс можно ускорить следующими приемами:
уменьшением Rк (и, следовательно, уменьшением постоянной времени Rк*С); однако при этом растут потребляемые от источника питания ток и мощность;
использованием в элементе малых перепадов напряжения;
применением на выходе элемента эмиттерного повторителя, уменьшающего влияние подключенной к выходу емкости нагрузки.
Помехоустойчивость определяется максимальным значением помехи, не вызывающей нарушения работы элемента.
Для количественной оценки помехоустойчивости воспользуемся так называемой передаточной характеристикой логического элемента (инвертора). На рис. 21 приведена типичная форма этой характеристики. Передаточная характеристика представляет собой зависимость выходного напряжения от входного. Для ее получения необходимо соединить все входы логического элемента и, изменяя напряжение на входе, отмечать соответствующие значения напряжения на выходе. При увеличении входного напряжения от нуля до порогового уровня лог. 0 -Un, напряжение на выходе уменьшается от уровня лог. 1 до некоторого минимально допустимого уровня лог. 1 – U1min. Дальнейшее увеличение входного напряжения приводит к резкому снижению выходного. При больших значениях входного напряжения, превышающих пороговый уровень лог. 1 U1min, на выходе устанавливается напряжение, не превышающее максимально допустимого уровня лог. 0 - U0max. Таким образом, при нормальной работе элемента в статическом (установившемся) режиме недопустимы входные напряжения U0п < Uвx <U1п.
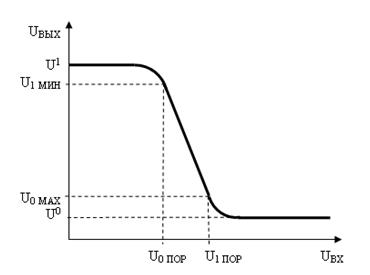
Рис. 21.
Допустимыми считаются такие помехи, которые, наложившись на входное напряжение, не выведут его в область недопустимых значений U0п < Uвx <U1п.
Дата добавления: 2016-05-31; просмотров: 3439;











