Интегрирование рациональных дробей

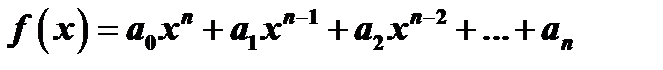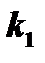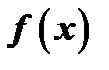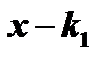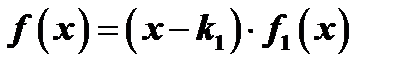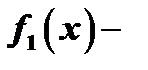Разложим многочлен , стоящий в знаменателе в произведение. Как известно из алгебры, всякий многочлен имеет по крайней мере один корень, действительный или мнимый (теорема Гаусса); обозначим этот корень через . Тогда, по теореме Безу, будет делиться без остатка на разность , т.е. , где многочлен степени 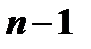. Продолжая эти процедуры так и далее получим разложение 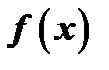в произведение:

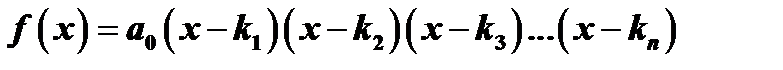
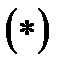
Разложение 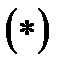показывает, что числа 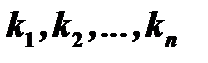являются корнями многочлена 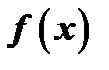и что, следовательно, многочлен 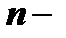ой степени не может иметь более чем 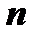различных корней, поскольку среди чисел 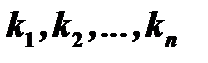могут быть и повторяющиеся. Если объединить множители, соответствующие повторяющимся корням, то разложение 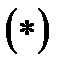примет вид:

,

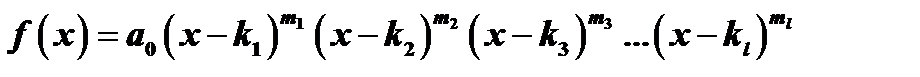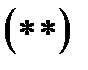
где 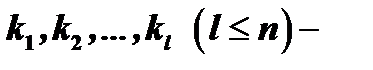попарно различные корни многочлена .

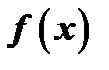Показатели степени 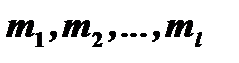называются кратностями корней 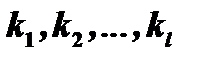. Легко видеть, что .

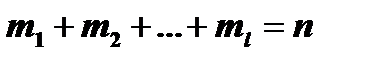Определение 1. Число 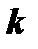называется 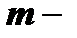кратным корнем многочлена 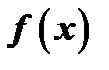, если 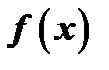делится без остатка на 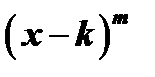, но не делится на .

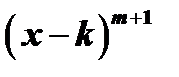Выберем среди всех попарно различных корней 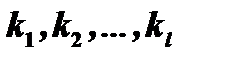многочлена 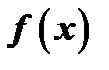действительные; пусть это будут корни 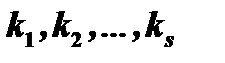с кратностями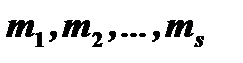 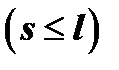. Тогда разложению 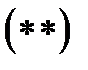можно придать следующий вид:

,

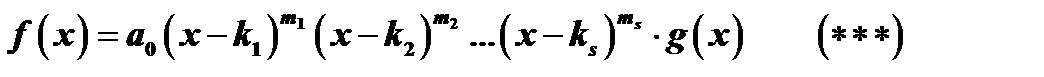где 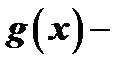многочлен с действительными коэффициентами степени 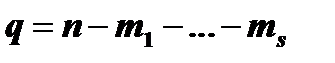, имеющий лишь комплексные корни.

Будем искать разложение многочлена 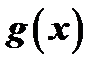на действительные множители, опираясь на следующую теорему:

Теорема. Комплексные корни всякого многочлена с действительными коэффициентами встречаются только сопряженными парами, причем сопряженные корни имеют одинаковую кратность.

Согласно этой теореме, в разложение 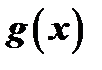сопряженные сомножител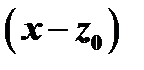и и 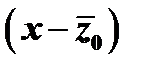входят в одинаковых степенях: 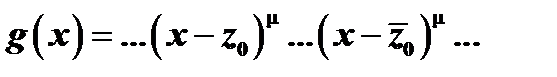. Используя это, перемножим эти двучлены, полагая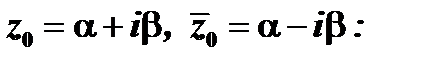

,

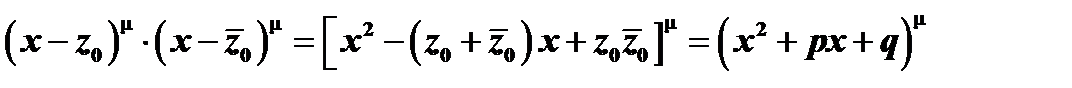где 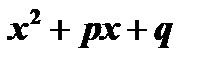есть квадратный трехчлен с действительными коэффициентами, имеющий мнимые корни. Проводя такую же операцию и со всеми остальными парами сопряженных сомножителей в разложении 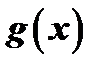, мы получаем разложение 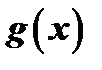на действительные множители: .

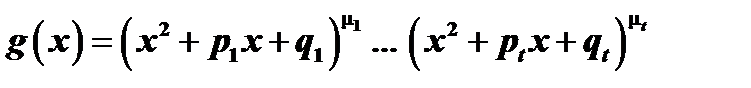Теперь, на основании равенства 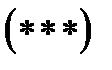, получим разложение многочлена 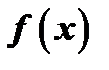на действительные множители:

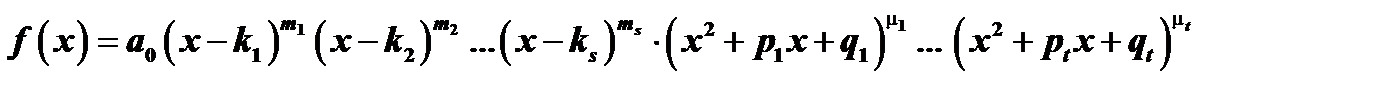
где 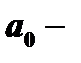коэффициент при старшей степени 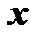в многочлене 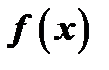, двучлены соответствуют действительным корням 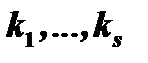многочлена 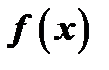, имеющим кратности 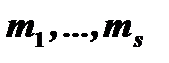, а трехчлены соответствуют парам сопряженных комплексных корней 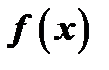кратностей .

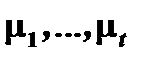Приведем без доказательства теорему алгебры о разложении рациональной дроби на сумму простейших дробей.

Теорема. Всякая правильная рациональная дробь может быть представлена, и притом единственным способом, в виде суммы конечного числа простейших дробей, вид которых определяется разложением знаменателя дроби в произведение действительных сомножителей:

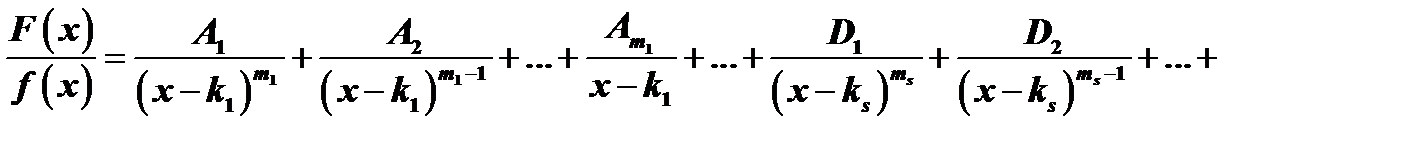
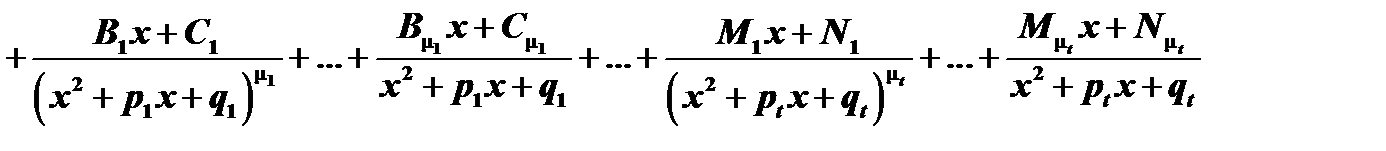
Неопределенные коэффициенты, стоящие в числителях простейших дробей разложения, находятся следующим образом. Приводим правую часть к общему знаменателю и обозначим приведенный числитель через 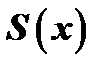: отбрасываем знаменатель как в левой, так и в правой части равенства, после чего получается тождество двух многочленов 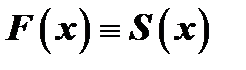, где 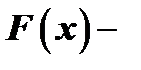известный многочлен, а многочлен 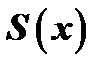содержит неопределенные коэффициенты. Приравнивая затем коэффициенты при одинаковых степенях 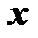в левой и правой частях тождества 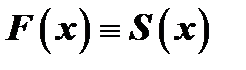, получим достаточное число совместных уравнений, линейных относительно неопределенных коэффициентов, откуда и найдем их числовые значения.

В дальнейшем интегрирование правильной рациональной дроби сводится к интегрированию простейших дробей 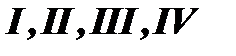типов.