Интегрирование тригонометрических функций

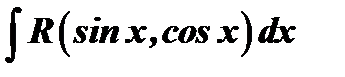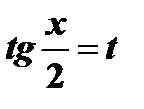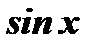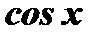Рассмотрим интеграл вида . Покажем, что этот интеграл с помощью подстановки всегда сводится к интегралу от рациональной функции. Выразим и через 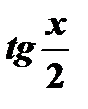, а следовательно, и через :

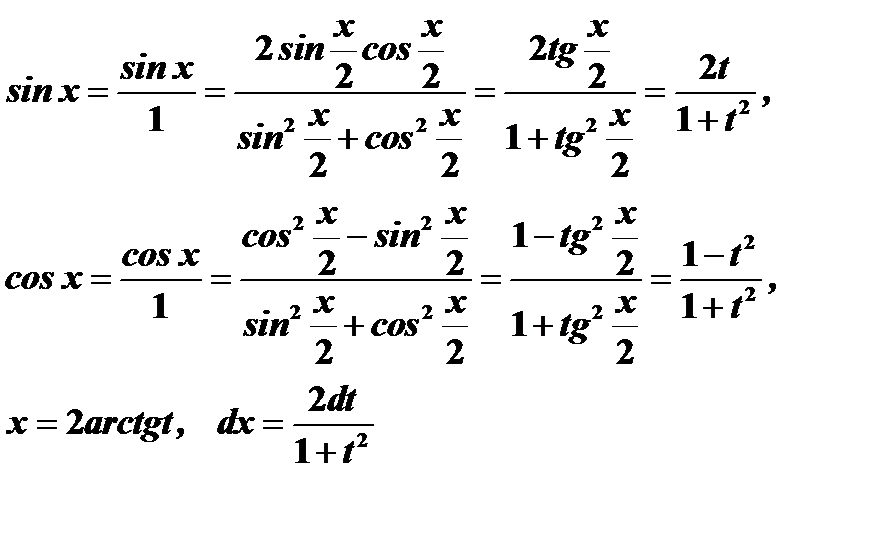
Таким образом .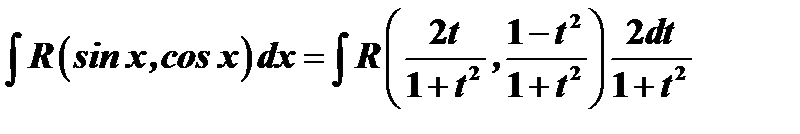

Рассмотренная подстановка дает возможность проинтегрировать всякую функцию вида 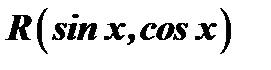. Поэтому ее иногда называют «универсальной тригонометрической подстановкой». Однако на практике она часто приводит к слишком сложным рациональным функциям. Поэтому наряду с «универсальной» подстановкой бывает полезно знать также другие подстановки, которые в некоторых случаях быстрее приводят к цели.

1)

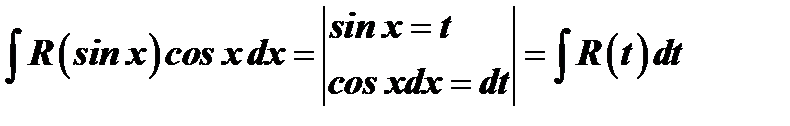
2)

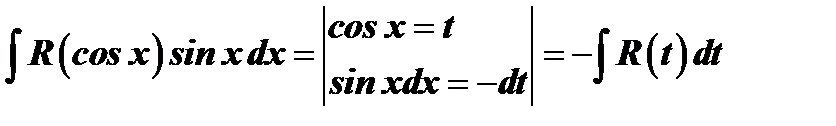
3)

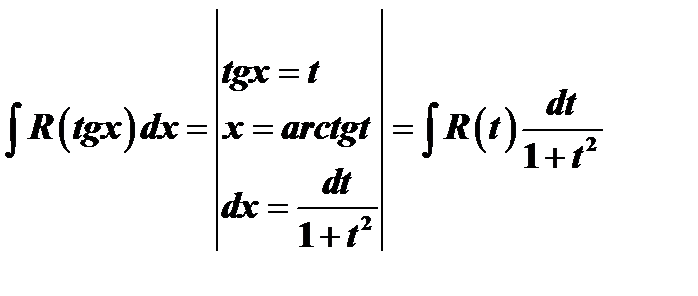
4)

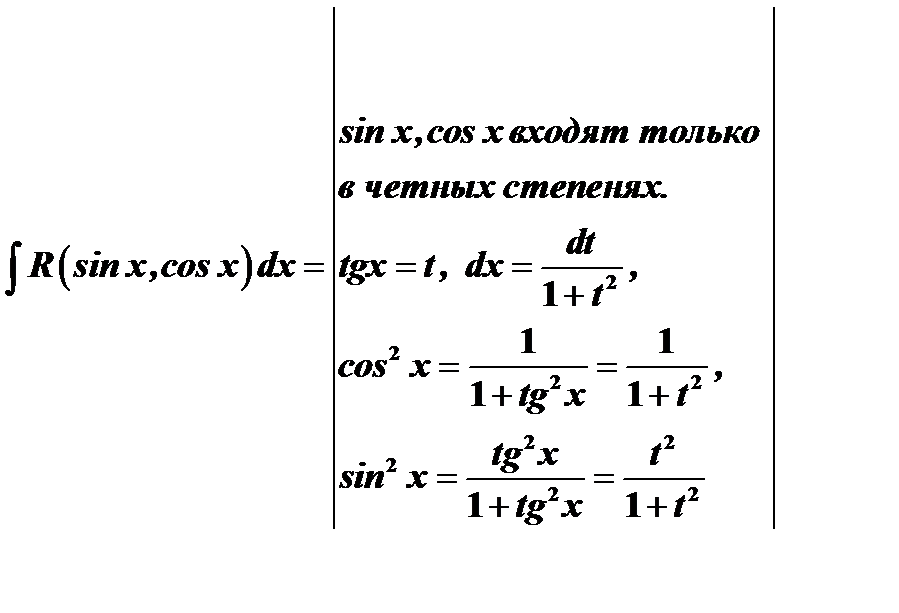
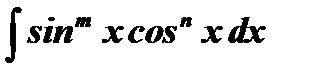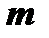5) , где и 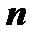таковы, что по крайней мере одно из них нечетное число. Допусти для определенности, что 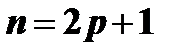, тогда

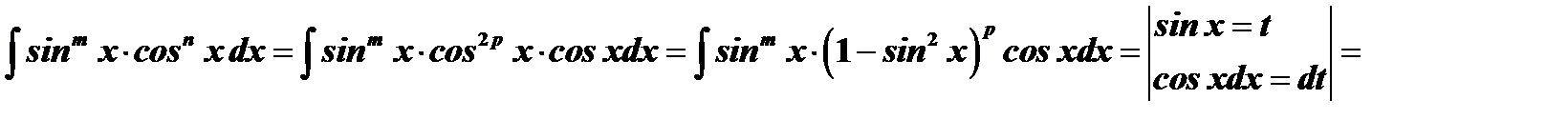
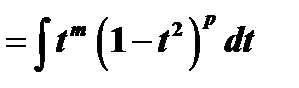
6)

Возводя в степень и раскрывая скобки, получим члены, содержащие 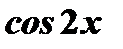в четных и нечетных степенях. Члены с нечетными степенями интегрируются, как указано в случае 5. Четные показатели степеней снова понижаются по формулам 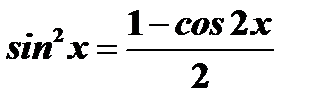и .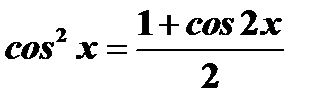

7) 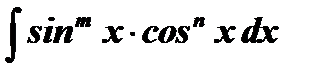. Если оба показателя – четные, причем хотя бы один из них отрицателен, то следует сделать замену 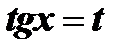или .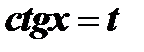

8) Интегралы вида 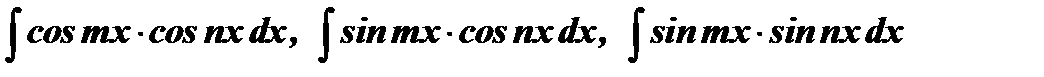вычисляются при помощи следующих формул :

.

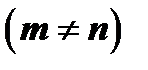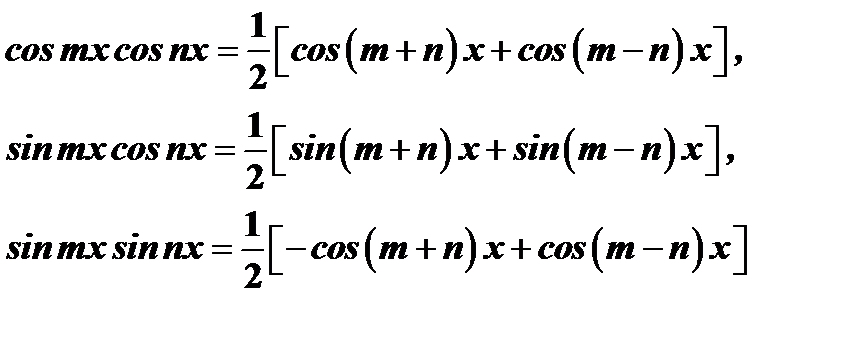
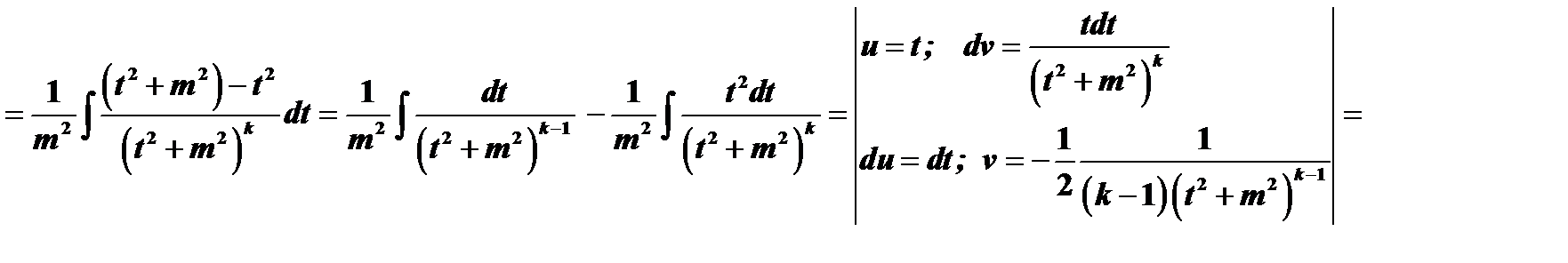
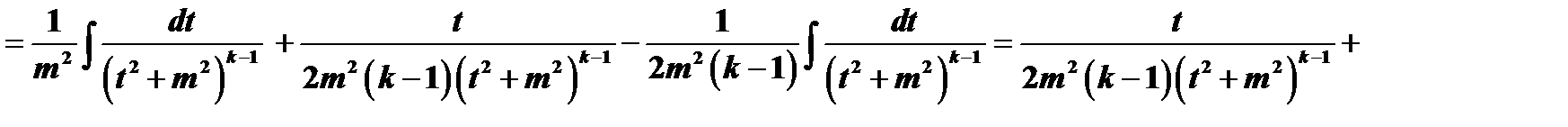
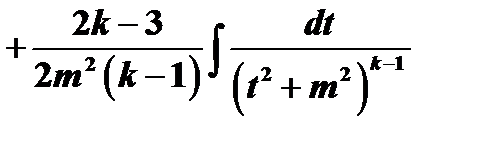В правой части содержится интеграл того же типа, что 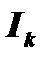, с той лишь разницей, что показатель степени знаменателя подынтегральной функции на единицу ниже 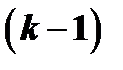; таким образом, мы выразили 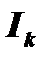через 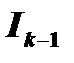. Продолжая идти тем же путем, дойдем до известного интеграла:

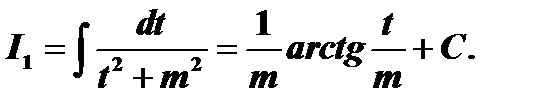
Подставляя затем всюду вместо и 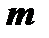значения, получим выражение интеграла 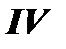через 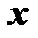и заданные числа А, В, p, q.

ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ