Комплексные числа и действия над ними
 Комплексным числом
Комплексным числом 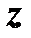 называется выражение вида
называется выражение вида 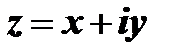 (алгебраическая форма комплексного числа), где
(алгебраическая форма комплексного числа), где 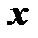 и
и 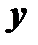 - любые действительные числа,
- любые действительные числа, 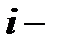 мнимая единица, удовлетворяющая условию
мнимая единица, удовлетворяющая условию 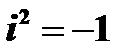 . Числа
. Числа 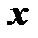 и
и 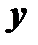 называются соответственно действительной и мнимой частями комплексного числа
называются соответственно действительной и мнимой частями комплексного числа 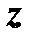 и обозначаются
и обозначаются 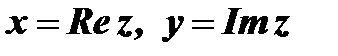 .
.
11) Комплексное число 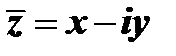 называется сопряженным комплексному числу
называется сопряженным комплексному числу 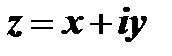 . Комплексные числа
. Комплексные числа 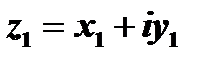 и
и 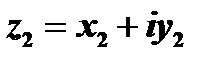 считаются равными тогда и только тогда, когда
считаются равными тогда и только тогда, когда 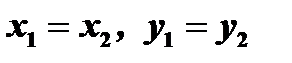 . Комплексное число
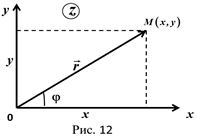
. Комплексное число 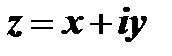 изображается в плоскости
изображается в плоскости 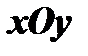 точкой
точкой 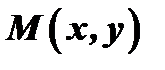 , либо вектором
, либо вектором  , начало которого находится в начале координат, а конец в точке
, начало которого находится в начале координат, а конец в точке 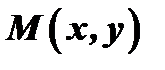 (рис.12). Длина вектора
(рис.12). Длина вектора  называется модулем комплексного числа и обозначается
называется модулем комплексного числа и обозначается 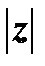 , так что
, так что 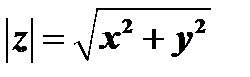 . Угол
. Угол 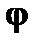 , образованный вектором
, образованный вектором  и осью
и осью 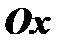 , называется аргументом комплексного числа
, называется аргументом комплексного числа 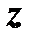 и обозначается
и обозначается 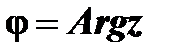 ; он определяется не однозначно, а с точностью до слагаемого, кратного
; он определяется не однозначно, а с точностью до слагаемого, кратного  :
: 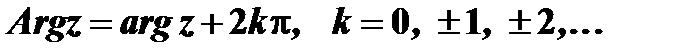 , где
, где 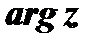 есть главное значение
есть главное значение 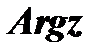 , определяемое условиями
, определяемое условиями 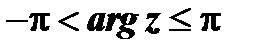 , причем
, причем
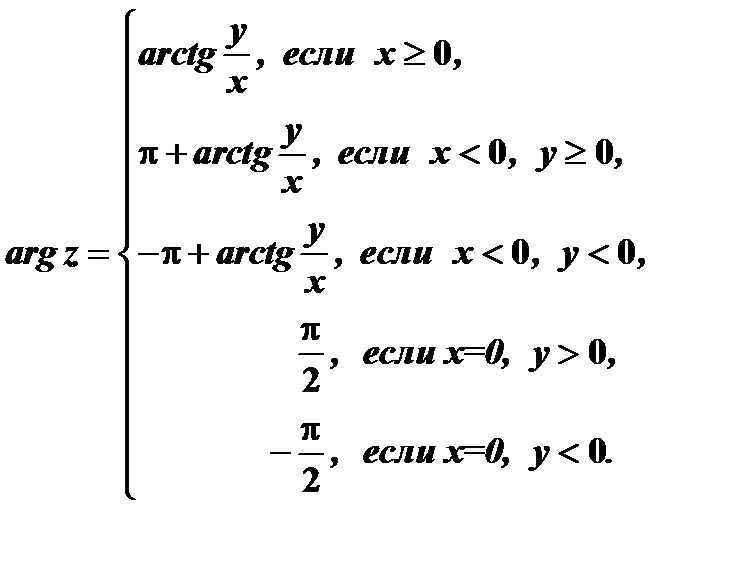
Тригонометрическая форма комплексного числа
Из рис.12 следует 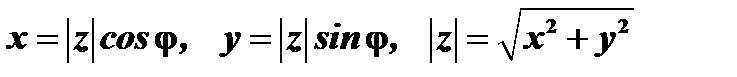 , следовательно
, следовательно 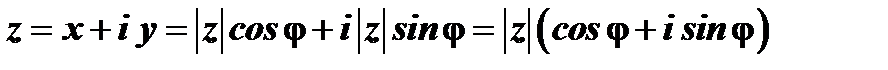 .
.
Тригонометрическая форма комплексного числа имеет вид
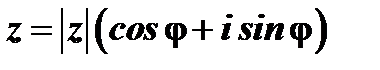
Дата добавления: 2017-10-04; просмотров: 1183;











