Первообразная и неопределённый интеграл
Дана функция 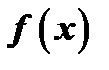 ; требуется найти такую функцию
; требуется найти такую функцию 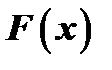 , производная которой была бы равна
, производная которой была бы равна 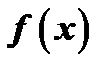 .
.
Определение 1. Функция 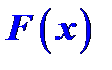 называется первообразной от функции
называется первообразной от функции 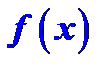 на отрезке
на отрезке 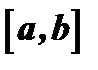 , если во всех точках этого отрезка выполняется равенство
, если во всех точках этого отрезка выполняется равенство 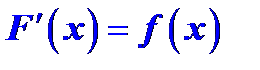 .
.
Так, например, для функции 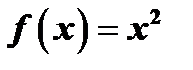 первообразной является функция
первообразной является функция 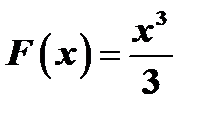 , т.к.
, т.к. 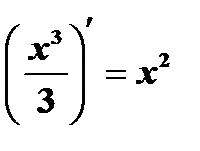 . Однако, легко заметить, что функции
. Однако, легко заметить, что функции 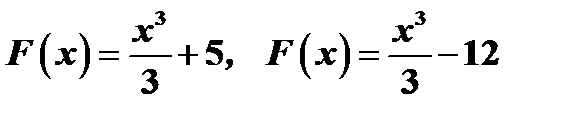 и вообще
и вообще 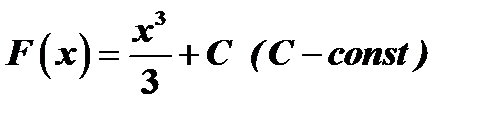 , так же являются первообразной функции
, так же являются первообразной функции 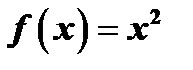 , т.к.
, т.к.
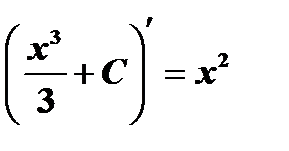 .
.
Определение 2. Если функция 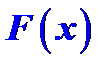 является первообразной для
является первообразной для 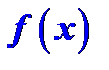 , то выражение
, то выражение 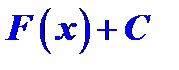 называется неопределённым интегралом от функции
называется неопределённым интегралом от функции 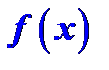 и обозначается символом
и обозначается символом 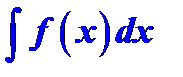 . Таким образом, по определению,
. Таким образом, по определению,
 .
.
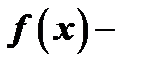 подынтегральная функция,
подынтегральная функция,
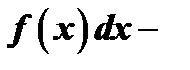 подынтегральное выражение,
подынтегральное выражение,
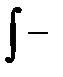 знак интеграла.
знак интеграла.
Нахождение первообразной для данной функции 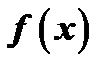 называется интегрированием функции
называется интегрированием функции 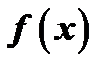 .
.
Из определения 2 следует:
1. Производная от неопределённого интеграла равна подынтегральной функции, т.е. если 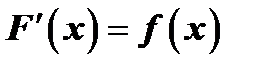 , то
, то 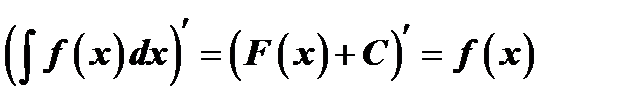 .
.
2. Дифференциал от неопределённого интеграла равен подынтегральному выражению, т.е. 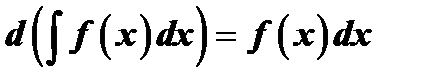 .
.
3. Неопределённый интеграл от дифференциала некоторой функции равен этой функции плюс произвольная постоянная, т.е. 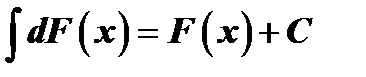 .
.
Неопределённый интеграл обладает следующими свойствами:
1. 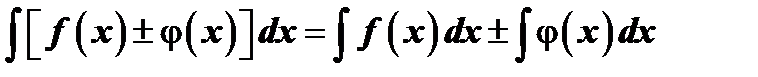 .
.
2. 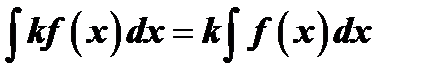
Таблица интегралов
| № | Основные формулы | Частный случай |
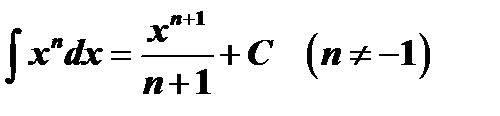
| 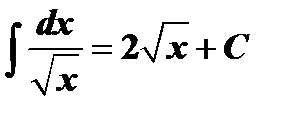
| |
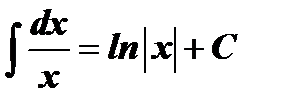
| ||
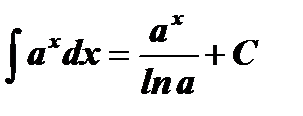
| 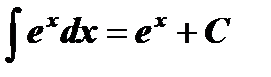
| |
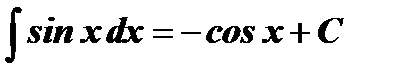
| 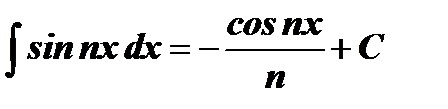
| |
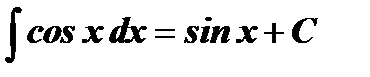
| 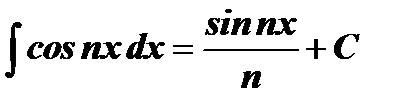
| |
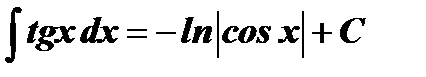
| ||
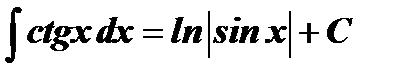
| ||
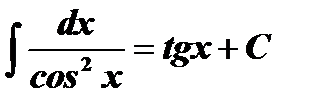
| 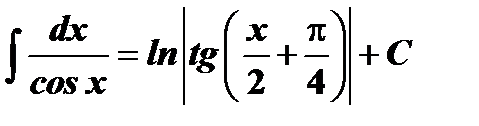
| |
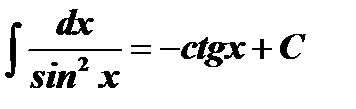
| 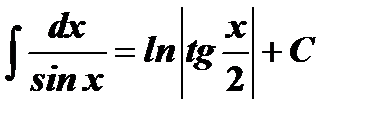
| |
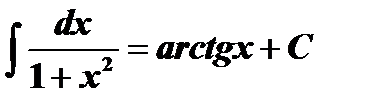
| ||
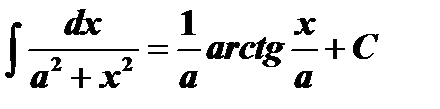
| ||
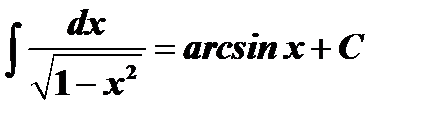
| ||
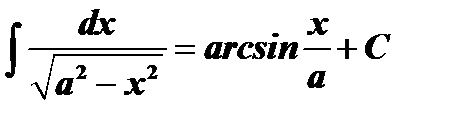
| ||
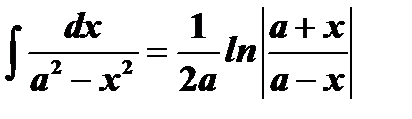
| 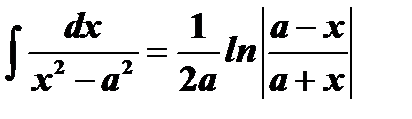
| |
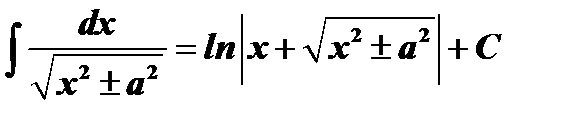
| ||
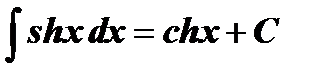
| ||
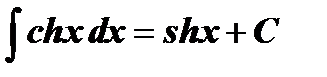
| ||
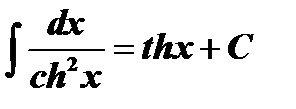
| ||
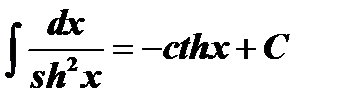
|
Дата добавления: 2017-10-04; просмотров: 1089;











