Интегрирование по частям

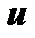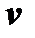Пусть и - дифференцируемые функции от 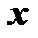. Тогда, как известно,

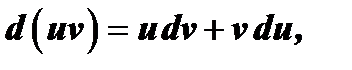
откуда следует

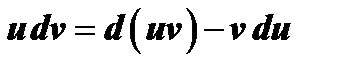
Интегрирование обеих частей этого равенства дает

.

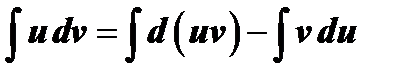Так как 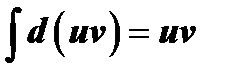, то получим

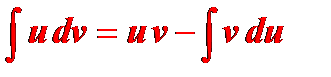
Это – формула интегрирования по частям, позволяющая переходить от заданного интеграла 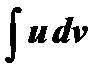к интегралу 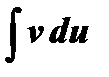; последний при удачном разбиении подынтегрального выражения на 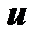и 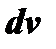может оказаться более простым, чем первоначальный.

Правило интегрирования по частям применяется во многих случаях. Эта формула часто применяется, когда подынтегральной функцией является логарифмическая или обратная тригонометрическая; произведение каждой из этих функций на алгебраическую; произведение, содержащее алгебраические, тригонометрические, показательные функции, и в некоторых других случаях.

Для интегралов вид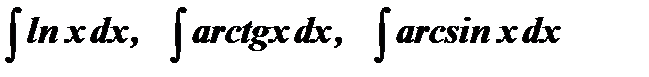а за 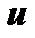принимается подынтегральная функция, а .

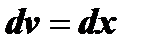Когда интегрирование по частям применяется к подынтегральной функции, имеющей вид произведения, то выбор множителей 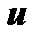и 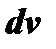должен соответствовать цели перехода к интегралу 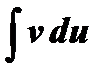, более простому, чем заданный интеграл 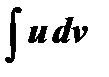, причем множитель 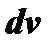, всегда включающий 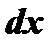, должен быть легко интегрируемым. Это достигается, например, тем, что для интегралов вид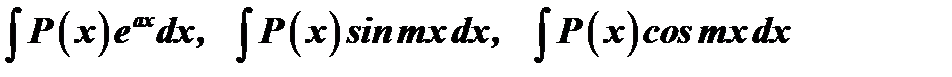а за 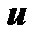принимается многочлен 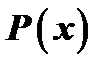, а для интегралов вид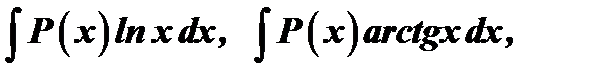а за 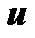принимается .

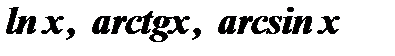Если в интегралах 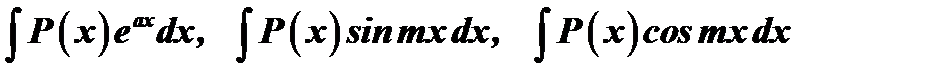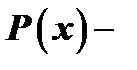многочлен выше первой степени, то операция интегрирования по частям приводит к результату лишь после применения ее несколько раз.