Потенциальная энергия деформации

При кручении

Представим себе круглый цилиндрический брус постоянного сече­ния, жестко защемленный одним концом и нагруженный на другом конце моментом, приложенным статически, т. е. медленно возрастающим от нуля до какого-то значения Т.Полагаем, что момент остается в пределах, когда нагрузка и деформация пропорциональны, т. е. справедлив закон Гука.

Момент T вызывает в брусе деформацию кручения и при этом со­вершает работу W, которая аккумулируется в виде потенциальной энер­гии деформации U,причем, пренебрегая незначительными потерями энергии, можно считать, что

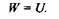
Как известно из теоретической механики, работа в случае статиче­ского нагружения равна

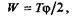
где 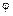— полный угол закручивания бруса. Так как Т = М_к, то

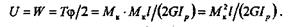
При одновременном действии нескольких моментов или ступенча­том изменении размеров поперечного сечения брус разбивают на участки и потенциальную энергию деформации всего бруса определяют как сум­му потенциальных энергий отдельных его участков:

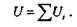
Анализируя полученную в этом параграфе формулу, можно сделать выводы, аналогичные выводам § 19.5.