Б) Модель сопротивления деформации

Согласно содержанию главы 2 (п.2.4), в качестве сопротивления деформация при холодной прокатке используют величину условного предела текучести, рассчитываемого по формуле А.В. Третьякова (2.22), причем в i-той рабочей клети n-клетевого стана график изменения условного предела текучести имеет вид, показанный на схеме “б” рисунка 6.2 в виде ломаной линии 1.

Перед входом в очаг деформации i-той клети полоса имеет условный предел текучести, согласно формуле (2.22), равный:

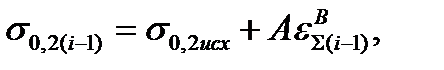(6.10)

где ε_Σ(i-1) – суммарное обжатие от исходного (недеформированного) состояния за предыдущие (i-1) проходов (после (i-1)-й клети);

σ_0,2(i-1) – значение σ_0,2, полученное в результате наклепа за (i-1) проходов.

После выхода из очага деформации i-й клети значение σ_0,2 увеличилось и стало, согласно той же формуле (2.22), равным:

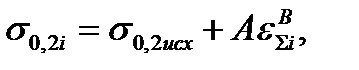(6.11)

где ε_Σi – суммарное обжатие за i проходов (после i-й клети).

Однако на 1-м упругом участке, согласно закону Гука (см. формулу (6.7) и график рис. 6.2.б), сопротивление деформации линейно возрастает от нуля до значения σ_0,2(i-1), достигая этого значения только в сечении ММ, на границе с пластическим участком. В этом сечении упругая деформация достигла значения Δh_1упр. Это значение легко найти, применив формулу (6.6) к первому упругому участку:

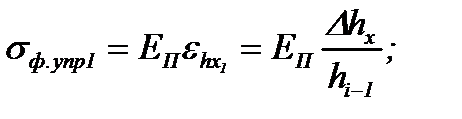(6.12)

где σ_ф.упр1 и ε_hx1 – сопротивление упругой деформации и относительная деформация сжатия материала полосы на первом упругом участке. Обе эти величины являются функциями координаты x или толщины полосы h_x.

В конце первого упругого участка, в сечении ММ σ_ф.упр1 = σ_0,2(i-1), Δh_x = Δh_1упр (см. рис. 6.2), поэтому из (6.12) получим:

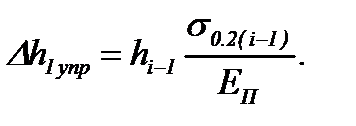(6.13)

Аналогично (6.12), на втором упругом участке сопротивление упругой деформации σ_ф.упр2 равно:

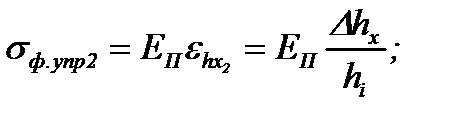(6.14)

где ε_hx2 – упругая деформация восстановления части толщины полосы в сечении с координатой x и толщиной h_x.

Абсолютная величина полного упругого приращения толщины полосы на этом участке, по аналогии с выражением (6.13), равна:

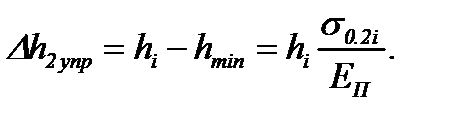(6.15)

Методики расчета контактных напряжений, изложенные в учебниках [1,2,3,6] и справочнике [4], исходили из того, что сопротивление деформации, равное σ_0,2(i-1), возникает в начале очага деформации, а величина σ_0,2i достигается не в конце пластического участка (сечение ВВ на рис. 6.2), а в конце очага деформации. Поэтому, согласно этим методикам, график изменения σ_0,2(h_x) по длине очага деформации выражается кривой 2, а не ломаной 1 на рис. 6.2,б. Если протяженность упругих участков относительно небольшая, погрешность энергосилового расчета от использования кривой 1, вместо ломаной 2, незначительна.

Но при холодной прокатке протяженность упругих участков может достигать 50-70% от общей длины очага деформации, поэтому использование в качестве графика сопротивления деформации кривой 2, вместо ломаной 1, приводит к погрешностям расчета контактных напряжений и усилий прокатки, достигающим 30-40% и более, что в технологических расчетах недопустимо.

Для расчета контактных напряжений в упругих и пластическом участках очага деформации используют среднее для каждого участка сопротивление деформации.

Согласно графику σ_ф на рис. 6.2,б, эти средние значения в i-й клети равны:

- на первом упругом участке:

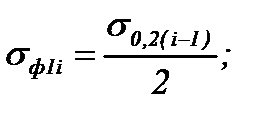(6.16)

- на втором упругом участке:

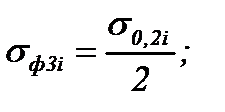(6.17)

- на пластическом участке, где сопротивление деформации выражается формулой А.В. Третьякова (2.22):

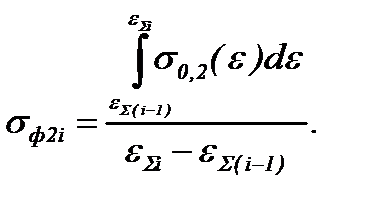(6.18)

Подставив под интеграл выражение σ_0,2(ε) по формуле (6.13) и проинтегрировав его, окончательно получим:

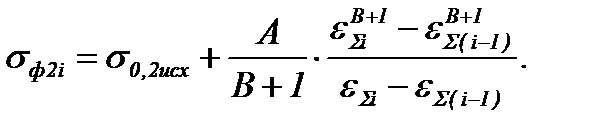(6.19)