Напряжения и деформации при кручении
Представим себе, что прямой круговой цилиндр, подвергаемый деформации кручения, состоит из бесконечно большого количества волокон, параллельных оси. Полагаем, что при кручении справедлива гипотеза о ненадавливании волокон.
Зная, что при кручении происходит деформация сдвига, естественно считать, что в точках поперечного сечения бруса возникают только касательные напряжения т, перпендикулярные радиусу, соединяющему эти точки с осью кручения. Существование нормальных напряжений в продольном сечении исключено, так как справедлива гипотеза о ненадавливании волокон; нормальные напряжения в поперечном сечении не возникают, так как нет продольной силы.
На рис. 22.1 видно, что абсолютный сдвиг сечения волокна а равен дуге аа1, а сечения волокна b — дуге bb1:
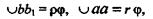
|
где 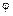 — полный угол закручивания, рад; r — радиус цилиндра;
— полный угол закручивания, рад; r — радиус цилиндра; 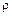 — расстояние от волокна b до оси кручения.
— расстояние от волокна b до оси кручения.
Так как радиусы сечения при кручении остаются прямыми, то величина абсолютного сдвига сечения волокон прямо пропорциональна их расстоянию от оси кручения.
Относительный сдвиг сечения волокна b
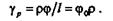
Применим формулу закона Гука при сдвиге:
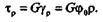
При 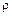 = 0
= 0 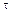 = 0, т. е. на оси кручения касательные напряжения равны нулю.
= 0, т. е. на оси кручения касательные напряжения равны нулю.
При 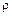 =
= 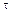
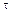 =
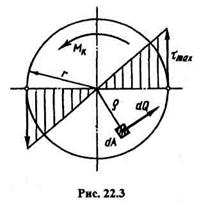
= 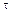 max, т. е. касательные напряжения достигают максимального значения у волокон, наиболее удаленных от оси кручения:
max, т. е. касательные напряжения достигают максимального значения у волокон, наиболее удаленных от оси кручения:
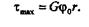
|
Так как относительный угол закручивания 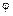 0 есть величина постоянная для данного цилиндрического бруса, то касательные напряжения при кручении прямо пропорциональны расстоянию от точек сечения до оси кручения. Эпюра распределения напряжений вдоль радиуса сечения имеет вид треугольника (рис. 22.3).
0 есть величина постоянная для данного цилиндрического бруса, то касательные напряжения при кручении прямо пропорциональны расстоянию от точек сечения до оси кручения. Эпюра распределения напряжений вдоль радиуса сечения имеет вид треугольника (рис. 22.3).
Если брус состоит из одного участка, т. е. имеет постоянное сечение и постоянный по длине участка крутящий момент, то касательные напряжения в данном волокне будут по всей длине цилиндра одинаковы.
Перейдем к выводу формул для определения угла закручивания и напряжений в поперечном сечении в зависимости от крутящего момента.
Рассечем брус, изображенный на рис. 22.1, поперечной плоскостью, находящейся на расстоянии z от заделки, и рассмотрим полученное сечение (рис. 22.3). Выделим в сечении бесконечно малую площадку dA на расстоянии 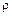 от оси кручения. Сила dQ, действующая на эту площадку, перпендикулярна радиусу и равна
от оси кручения. Сила dQ, действующая на эту площадку, перпендикулярна радиусу и равна
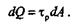
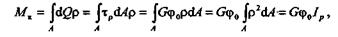
|
| откуда найдем относительный угол закручивания: |
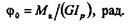
|
| Полный угол закручивания цилиндра длиной l: |
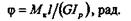
|
Определим момент внутренних сил относительно оси кручения, т. е. крутящий момент:
Произведение GIp, стоящее в знаменателе, называется жесткостью сечения при кручении.
Итак, мы установили, что полный угол закручивания круглого цилиндра прямо пропорционален крутящему моменту, длине цилиндра и обратно пропорционален жесткости сечения при кручении.
Так как при выводе последней формулы мы применяли закон Гука, она справедлива в пределах, когда нагрузка и деформация прямо пропорциональны.
Для цилиндрического бруса, имеющего несколько участков, отличающихся материалом, размерами поперечного сечения, значением крутящего момента, полный угол закручивания равен алгебраической сумме углов закручивания отдельных участков:
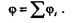
Выведем формулу для определения напряжений:
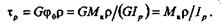
При 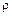 = r напряжения достигнут максимального значения:
= r напряжения достигнут максимального значения:
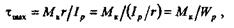
где Wp =Ip/r— момент сопротивления сечения кручению (или полярный момент сопротивления).
Момент сопротивления кручению равен отношению полярного момента инерции к радиусу сечения.
Единица момента сопротивления кручению
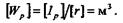
Итак, напряжения и деформации при кручении круглого цилиндра вычисляют по формулам
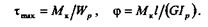
Обратим внимание на то, что эти формулы по структуре аналогичны формулам для вычисления напряжений и деформаций при растяжении, сжатии и применимы лишь для участков бруса, имеющих одинаковый материал, постоянные поперечное сечение и крутящий момент.
По закону парности касательных напряжений, последние возникают не только в поперечных, но и в продольных сечениях, поэтому, например, в деревянных брусьях при кручении возникают трещины вдоль волокон (древесина плохо работает на скалывание вдоль волокон).
Из эпюры распределения касательных напряжений при кручении видно, что внутренние волокна бруса испытывают небольшие напряжения, поэтому валы иногда делают пустотелыми, чем достигается значительный выигрыш в массе при незначительной потере прочности.
Определим момент сопротивления кручению для круглого и кольцевого сечений.
1. Круг диаметром d:
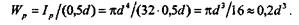
2. Кольцо размером D 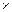 d:
d:
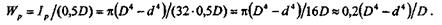
Отметим, что если полярный момент инерции кольцевого сечения можно определить как разность моментов инерции большого и малого кругов, то момент сопротивления кручению нельзя определять как разность моментов сопротивлений этих кругов.
Пример 22.2. Стальной пруток длиной l= 1 м, диаметром d = 4 мм одним концом укреплен в зажиме, а на другом приложен скручивающий момент. При каком угле закручивания напряжение кручения будет равно 120 МПа? Модуль упругости второго рода G = 8,2  104 МПа.
104 МПа.
Решение. Запишем формулы, необходимые для решения задачи: полный угол закручивания круглого цилиндра
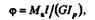
|
максимальное напряжение при кручении
| откуда |
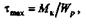
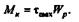
Учитывая, что полярный момент инерции
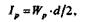

и подставляя числовые значения, получаем
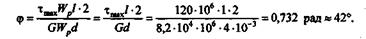
|
Дата добавления: 2021-09-07; просмотров: 488;











