Расчет цилиндрических винтовых пружин
В технике наиболее распространены цилиндрические винтовые пружины из стали круглого поперечного сечения, работающие на растяжение или сжатие. В данном параграфе рассмотрен расчет таких пружин, имеющих небольшой угол а подъема витков ( 
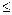 15°).
15°).
Рассмотрим цилиндрическую винтовую пружину с диаметром D винтовой оси, диаметром d проволоки и количеством витков п,сжимаемую силой F (рис. 22.4, а).
Для определения внутренних силовых факторов применим метод сечений. Рассечем пружину плоскостью, проходящей через ось, и отбросим нижнюю часть пружины (рис. 22.4, б). Ввиду того что угол а подъема витков мал, будем считать сечение витка поперечным, т. е. кругом диаметра d
Рассматривая равновесие верхней части пружины, видим, что в поперечном сечении витка возникают два внутренних силовых фактора: поперечная сила Q = F и крутящий момент Мк= FD/2.Отсюда следует, что в поперечном сечении витка действуют только касательные напряжения сдвига и кручения.
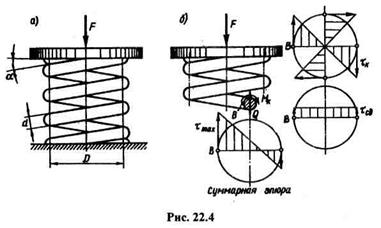
Будем считать, что напряжения сдвига распределены по сечению равномерно, а напряжения кручения определяются, как при кручении прямого кругового цилиндра. Эпюры распределения напряжений сдвига и кручения, а также эпюра суммарных напряжений в точках горизонтального диаметра сечения представлены на рис. 22.4, б.
Из суммарной эпюры видно, что наибольшие касательные напряжения возникают в точке В,ближайшей к оси пружины:
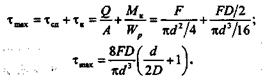
|
Если пружина имеет относительно большой средний диаметр и изготовлена из относительно тонкой проволоки, то первое слагаемое в скобках (соответствующее напряжению сдвига) значительно меньше единицы и им можно пренебречь; тогда
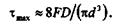
(22.1)
Формула для приближенного расчета цилиндрических винтовых пружин имеет вид
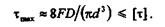
Так как пружины обычно изготовляют из высококачественной стали, допускаемое напряжение берут в пределах
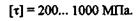
Далее выведем формулу для определения уменьшения высоты (осадки) 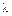 пружины. Разбивая пружину на бесконечно малые участки длиной dl, которые ввиду малости длины будем считать прямолинейными, и учитывая только потенциальную энергию деформации кручения, получим:
пружины. Разбивая пружину на бесконечно малые участки длиной dl, которые ввиду малости длины будем считать прямолинейными, и учитывая только потенциальную энергию деформации кручения, получим:
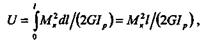
|
где l = 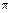 Dп — длина проволоки пружины.
Dп — длина проволоки пружины.
Работа силы F,приложенной к пружине статически, будет равна W =
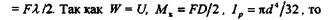
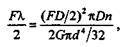
|
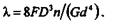
|
| откуда |
Эту формулу можно записать в таком виде:
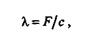
|
где с = Gd4/(8D3n)— коэффициент жесткости пружины.
При 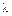 = 1 с = F,поэтому коэффициент жесткости численно равен силе, вызывающей осадку, равную единице длины.
= 1 с = F,поэтому коэффициент жесткости численно равен силе, вызывающей осадку, равную единице длины.
Отношение среднего диаметра витков к диаметру проволоки обозначают спи называют и н д е к с о м пружины:

Обычно индекс пружины бывает в пределах сп = 4...12.
При более точных расчетах винтовых пружин учитывают кривизну их витков и вводят в числитель формулы (22.1) поправочный коэффициент
К 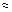 1 + 1,45/сп.
1 + 1,45/сп.
Пример 22.5. Определить диаметр проволоки стальной пружины, если под действием силы F = 800 Н ее осадка 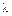 = 39 мм. Индекс пружины сп= 6, число витков п = 14. Модуль упругости G = 8
= 39 мм. Индекс пружины сп= 6, число витков п = 14. Модуль упругости G = 8  104 МПа, допускаемое напряжение [
104 МПа, допускаемое напряжение [ 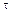 ] = 450 МПа.
] = 450 МПа.
Решение. Индекс пружины сп= 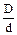 , откуда D = сп d. Подставим значение D в формулу для осадки пружины:
, откуда D = сп d. Подставим значение D в формулу для осадки пружины:
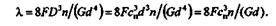
|
| Отсюда находим d и после подстановки числовых значений получаем |
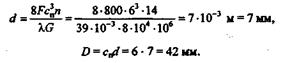
Глава 23
ИЗГИБ
Дата добавления: 2021-09-07; просмотров: 978;











