Дифференциальные зависимости при изгибе
Между изгибающим моментом, поперечной силой и интенсивностью распределенной нагрузки существуют дифференциальные зависимости, основанные на теореме Журавского, названной по имени замечательного русского инженера-мостостроителя Д. И. Журавского (1821—1891). Эта теорема формулируется так: поперечная сила равна первой производной от изгибающего момента по абсциссе сечения балки.
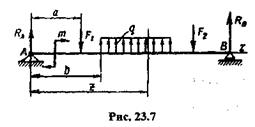
Рассмотрим балку (рис. 23.7). Начало координат возьмем на левом конце балки, а ось z направим вправо (в дальнейшем это будет иметь существенное значение).
|
На одном из участков балки возьмем сечение с текущей координатой z и запишем уравнение изгибающего момента:
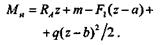
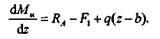
|
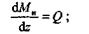
|
| Продифференцировав это выражение по координате z, получим |
| Выражение, стоящее в правой части этого равенства, есть поперечная сила Q в сечении z.Таким образом, |
теорема доказана.
Если уравнение изгибающих моментов (для участков с равномерно распределенной нагрузкой) продифференцировать вторично, то получим
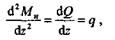
т. е. вторая производная от изгибающего момента или первая производная от поперечной силы по абсциссе сечения балки равна интенсивности распределенной нагрузки.
Как известно из высшей математики, по знаку второй производной функции можно судить о выпуклости или вогнутости кривой; соответствующее правило следует использовать при построении эпюр.
Дата добавления: 2021-09-07; просмотров: 663;











