Изгибающий момент и поперечная сила

Как известно из теоретической механики, опорные реакции балок определяют, составляя для всей балки и решая уравнения равновесия ста­тики. Будем помнить, что при определении внутренних сил реакции свя­зей учитываются наравне с активными внешними силами, действующими на балку.

Для определения внутренних силовых факторов применим метод се­чений, причем изображать балку будем только одной линией — осью, к которой приложены активные и реактивные силы. Рассмотрим два случая:

1. К балке приложены две равные и противоположные по знаку пары сил (рис. 23.3).

Рассматривая равновесие части балки, расположенной слева или справа от сечения 1—1, видим, что во всех поперечных сечениях возни­кает только изгибающий момент М_и, равный внешнему моменту. Таким образом, рассматриваемый случай есть случай чистого изгиба.

Изгибающий момент есть результирующий момент относительно нейтральной оси внутренних нормальных сил, действующих в попереч­ном сечении балки.

Обратим внимание на то, что изгибающий момент имеет разное на­правление для левой и правой частей балки. Это говорит о непригодности правила знаков статики при определении знака изгибающего момента.

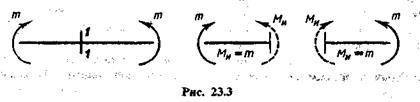
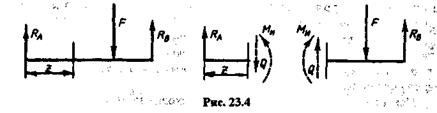
2. К балке приложены активные и реактивные силы, перпен­дикулярные оси (рис. 23.4).

Рассматривая равновесие частей балки, расположенных слева и справа, видим, что в поперечных сечениях должны действовать изгибаю­щий момент М_ии поперечная сила Q.Из этого следует, что в рассматри­ваемом случае в точках поперечных сечений действуют не только нор­мальные напряжения, соответствующие изгибающему моменту, но и ка­сательные, соответствующие поперечной силе.

Поперечная сила есть равнодействующая внутренних касательных сил в поперечном сечении балки.

Обратим внимание на то, что поперечная сила имеет противополож­ное направление для левой и правой частей балки, что говорит о непри­годности правила знаков статики при определении знака поперечной силы.

Изгиб, при котором в поперечном сечении балки действуют изги­бающий момент и поперечная сила, называется поперечным.

Нетрудно видеть, что в общем случае при поперечном изгибе изги­бающий момент и поперечная сила в разных сечениях могут иметь не­одинаковое значение.

У балки, находящейся в равновесии под действием плоской системы сил, алгебраическая сумма моментов всех активных и реактивных сил относительно любой точки равна нулю; следовательно, сумма моментов внешних сил, действующих на балку левее сечения, численно равна сум­ме моментов всех внешних сил, действующих на балку правее сечения.

Таким образом, изгибающий момент в сечении балки численно равен алгебраической сумме моментов относительно центра тяжести сече­ния всех внешних сил, действующих справа или слева от сечения.

У балки, находящейся в равновесии под действием плоской системы сил, перпендикулярных оси (т. е. системы параллельных сил), алгебраи­ческая сумма всех внешних сил равна нулю; следовательно, сумма внеш­них сил, действующих на балку левее сечения, численно равна сумме сил, действующих на балку правее сечения.

Таким образом, поперечная сила в сечении балки численно равна ал­гебраической сумме всех внешних сил, действующих справа или слева от сечения.

Так как правила знаков статики неприемлемы для установления зна­ков изгибающего момента и поперечной силы, установим для них другие правила знаков, а именно:

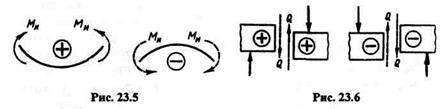
если внешняя нагрузка стремится изогнуть балку выпуклостью вниз, то изгибающий момент в сечении считается положительным, и наобо­рот, если внешняя нагрузка стремится изогнуть балку выпуклостью вверх, то изгибающий момент в сечении считается отрицательным (рис. 23.5);

если сумма внешних сил, лежащих по левую сторону от сечения, да­ет равнодействующую, направленную вверх, то поперечная сила в сече­нии считается положительной, если равнодействующая направлена вниз, то поперечная сила в сечении считается отрицательной; для части балки, расположенной справа от сечения, знаки поперечной силы будут проти­воположными (рис. 23.6).

Пользуясь этими правилами, следует мысленно представлять себе сечение балки жестко защемленным, а связи отброшенными и заменен­ными реакциями.

Подчеркнем, что для определения опорных реакций пользуются пра­вилами знаков статики; для определения знаков изгибающего момента и поперечной силы — правилами знаков сопротивления материалов.

Правило знаков для изгибающих моментов иногда называют «прави­лом дождя» (имея в виду, что в случае выпуклости вниз образуется во­ронка, в которой задержится дождевая вода, и наоборот).