Б) Модель сопротивления деформации
В соответствии с общими положениями о влиянии сопротивления деформации на контактные напряжения, изложенными в п. 6.2, для определения сопротивления деформации в процессе горячей прокатки можно использовать либо формулу В.И. Зюзина (2.20), либо формулу Л.В. Андреюка (2.21) (глава 2). Предпочтительнее формула (2.21), т.к. в справочнике [23], где она приводится, дан более широкий сортамент марок сталей и сплавов, чем для формулы (2.20), приводимой в справочниках [4;24]. С точки зрения теории пластической деформации эти формулы равнозначны, т.к. выражают зависимость сопротивления деформации σф от совокупности одних и тех же параметров: базисного сопротивления деформации σо.д, определяемого химическим составом стали, температуры прокатываемой полосы, суммарного обжатия и скорости деформации.
Сопротивление деформации изменяется по мере продвижения полосы через очаг деформации, т.к. при этом изменяются температура и суммарное обжатие. Эти изменения происходят одновременно в противоположенных направлениях: из-за обжатия σф растет в результате наклепа, а из-за высокой температуры σф уменьшается в результате рекристаллизации.
Поэтому обычно принято определять по формуле (2.21) или (2.20) среднее значение σф для всего очага деформации и его использовать в расчете контактных напряжений как постоянную исходную величину.
Например, для i-й рабочей клети ШПСГП формула Л.В. Андреюка (2.21) будет иметь вид:
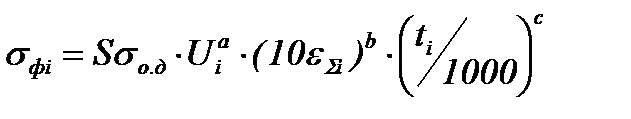 , (6.62)
, (6.62)
где σфi – среднее значение сопротивления пластической деформации в i-й рабочей клети (при толщине подката h0, толщине полосы на выходе из i-й клети hi);
σод – базисное значение сопротивления деформации (при температуре полосы 1000оС, обжатии 0,1 (10%) и скорости деформации 1 1/c);
ui, 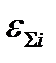 - соответственно: скорость деформации (1/c) и суммарное относительное обжатие от толщины h0 до толщины hi в 2-й клети (безразмерное);
- соответственно: скорость деформации (1/c) и суммарное относительное обжатие от толщины h0 до толщины hi в 2-й клети (безразмерное);
S, a, b, c – постоянные числа, зависящие от марки стали, сплава (приведены в справочнике [23]);
ti – температура полосы на выходе из i-й клети,
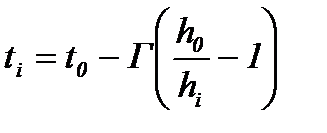 ,
,
t0 – температура подката;
Г – градиент температуры:
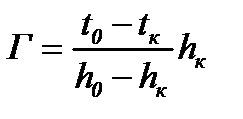 ,
,
tк, hк – температура и толщина готового проката (на выходе из последней клети ШПСГП).
Модель сопротивления деформации, предлагаемая в данном учебнике, отличается от других моделей тем, что формула σфi (6.62) (или аналогичная ей формула В.И. Зюзина) применяется для расчета контактных напряжений не на всей протяженности очага деформации, а только на его пластической части. На упругих участках, как и в очагах деформации стана холодной прокатки, вместо сопротивления пластической деформации надо использовать сопротивление упругой деформации, под которым понимается напряжение в испытуемом образце на упругом участке его нагружения. Это напряжение, согласно закону Гука, изменяется линейно от нуля до σфi, поэтому на упругих участках в качестве сопротивления деформации можно принять его среднее значение:
σфiупр=0,5 σфi (6.63)
в) Модель коэффициента трения.
Из графика изменения по длине очага деформации напряжений τx (рис. 6.16) и формул (6.59), (6.614), принятых в качестве четвертого допущения для расчета контактных напряжения, видно, что коэффициент трения μ при горячей прокатке влияет на величину контактных напряжений только на упругих участках очага деформации стана горячей прокатки. Для этих участков на основе анализа известных эмпирических формул коэффициента трения можно рекомендовать как наиболее достоверную формулу [23]:
μi=k1k2k3(1,05-0,0005ti), (6.64)
где k1 – коэффициент, учитывающий состояние поверхности и материал валков;
k2 – коэффициент, учитывающий скорость прокатки;
k3 – коэффициент, учитывающий содержание углерода в стали.
Значения этих коэффициентов приведены в справочнике [23].
г) Система уравнений для получения расчетных формул контактных напряжений.
Принцип вывода расчетных формул контактных напряжений в очаге деформации рабочей клети ШПСГП такой же, как и для стана холодной прокатки (см. п. 6.3, г): для каждого участка очага деформации составляют систему трех уравнений.
Первое:дифференциальное уравнение равновесия элемента полосы, с использованием схемы напряжений, показанной на рис. 6.2, а:
ΣXi=0, (6.65)
где Xi – проекции на ось x (ось прокатки) всех сил, приложенных к элементу abdc снаружи, через площадки ab, bd, cd, ac, в результате суммирования на этих площадках напряжений px(hx), τx(hx), σx(hx), (σx+d σx)(hx+dhx) (см. табл. 6.2)
Второе: уравнение касательных напряжений:
- на упругих участках уравнение (6.59);
- на пластическом участке уравнение (6.61), общее для зон отставания и опережения.
Третье: уравнение пластичности (на пластическом участке) или упругости (на упругих участках).
Эти уравнения имеют такой же вид, как и в очаге деформации стана холодной прокатки (см. п. 6.3, г, уравнения (6.23), (6.24), (6.25), там же подробно объяснена методика их вывода, основанная на допущениях, введенных в теорию прокатки А.И. Целиковым). Перепишем их с учетом специфики процесса горячей прокатки.
- уравнение упругости для 1го упругого участка:
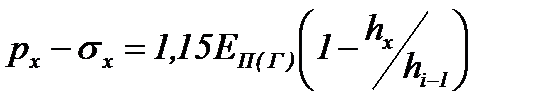 , (6.66)
, (6.66)
- уравнение пластичности для пластического участка:
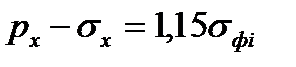 , (6.67)
, (6.67)
- уравнение упругости для 2го упругого участка:
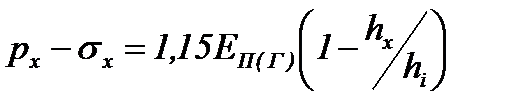 , (6.68)
, (6.68)
где EП(Г) – модуль упругости материала полосы в температурном интервале горячей прокатки, который по справочным данным [24], на 25-30% меньше, чем при холодной прокатке;
σфi – среднее значение сопротивления пластической деформации, вычисляемое, например, по формуле (6.62).
д) Решение системы уравнений – получение расчетных формул px(hx), τx(hx), σx(hx) для очага деформации ШПСГП.
Составление и решение указанной выше системы уравнений выполняется теми же методами, что и для очага деформации стана холодной прокатки.
Опыт расчетов показал, что при горячей прокатке в очаге деформации всегда есть нейтральное сечение, причем оно является единственным. Поэтому ход решения аналогичен изложенному в п. 6.3, г, д.
Изучающим теорию прокатки рекомендуется проделать это решение самостоятельно, это позволит глубже осмыслить методику расчета контактных напряжений.
Исходные уравнения для формулы px(hx) и их окончательные выражения приведены для упругих участков в табл. 6.8, для пластического участка – в табл. 6.9.
Таблица 6.8
Основные выражения, характеризующие упругие участки очага деформации i-й рабочей клети при горячей прокатке тонких широких полос.
| Участок упругого сжатия длиной x1упр | Участок упругого восстановления длиной x2упр |
| 1. Дифференциальные уравнения равновесия | |
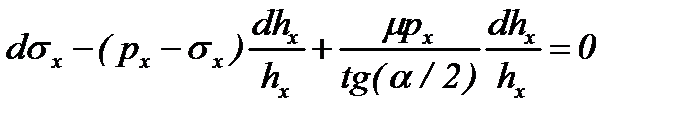 , где , где 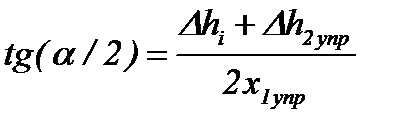
| 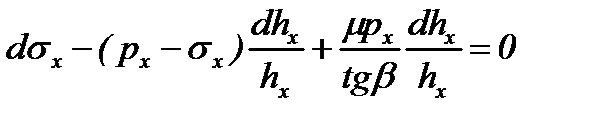 ,
где ,
где 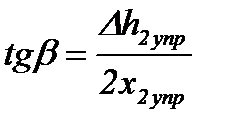
|
| 2. Уравнения упругости | |
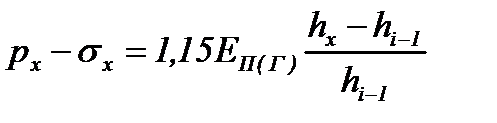
| 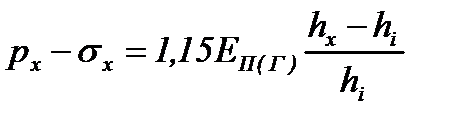
|
| 3. Закон трения | |
| τx=μipx | |
| 4. Формулы px(hx) | |
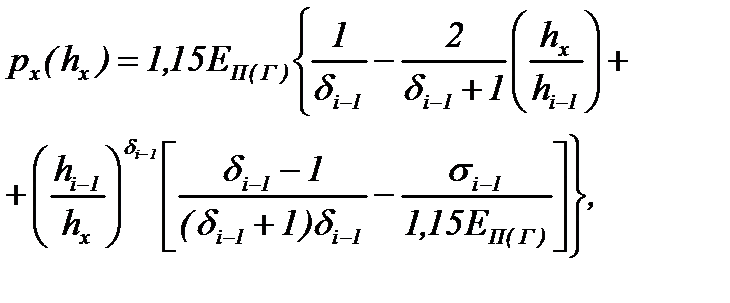 где
где 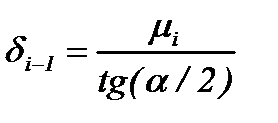
| 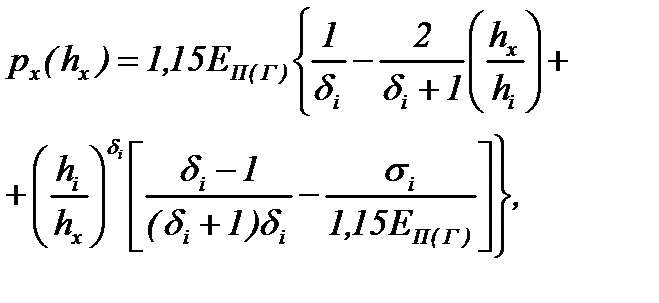 где где 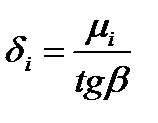
|
Примечание. hi-1 – толщина полосы на входе в i-ю клеть; σi-1, σi – заднее и переднее удельные натяжения; углы α/2 и β – см. рис. 6.16.
В связи с некоторой громоздкостью формул px(hx) их применение требует использования компьютера.
Формулы px(hx) для упругих участков (табл. 6.8, п. 4) аналогичны соответствующим формулам очага деформации стана холодной прокатки (табл. 6.3). Их разница только в значениях модуля упругости полосы: величина EП(Г) в табл. 6.8 меньше величины EП в табл. 6.3:
EП(Г)≈(0,7-0,75) EП.
Формула px(hx) для пластического участка (табл. 6.9, п. 4) существенно отличается от соответствующих формул для очага деформации стана холодной прокатки из-за разницы условий трения: при горячей прокатке на пластическом участке, согласно принятому допущению, действуют напряжения трения покоя τx, характерные для зоны прилипания, выражаемые формулой (6.61) (табл. 6.9, п. 3). Поэтому в формуле px(hx) (табл. 6.9, п. 4) отсутствует коэффициент трения и эта формула единая для зоны отставания и опережения.
Таблица 6.9.
Основные выражения, характеризующие пластический участок очага деформации i-й рабочей клети при горячей прокатке тонких широких полос.
| 1. Дифференциальное уравнение равновесия | 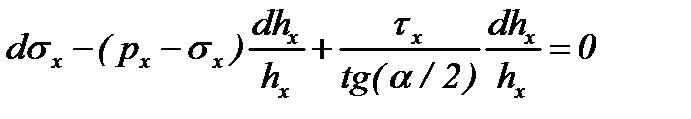
|
| 2. Уравнение пластичности | 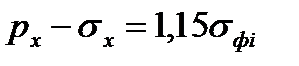
|
| 3. Напряжение трения | 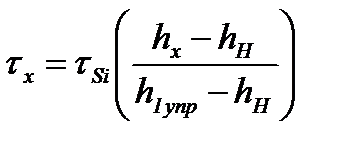
|
| 4. Формула px(hx) | 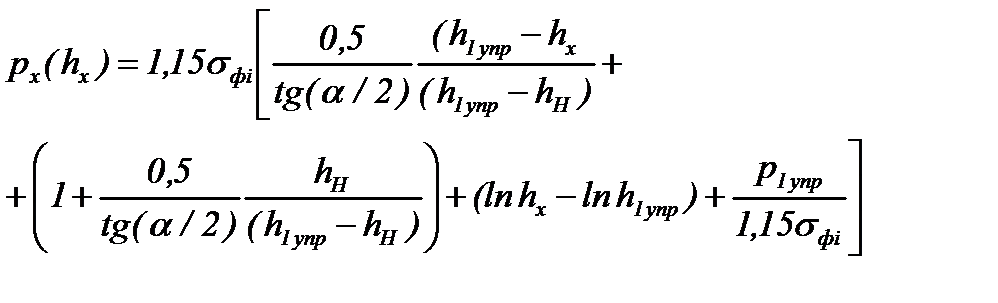
|
Примечание. p1упр – значение нормального контактного напряжения, рассчитанное по уравнению px(hx) для первого упругого участка в сечении, где hx=h1упр, τSi=0,57σфi – среднее сопротивление чистого сдвига в i-й рабочей клети, hН – толщина полосы в нейтральном сечении.
В качестве граничных условий на входе и выходе очага деформации при решении дифференциальных уравнений на упругих участках используют заданные удельные натяжения полосы σi-1, σi. В качестве граничного условия для пластического участка используют значение px(hx), рассчитанное для первого упругого участка в сечении, где hx=h1упр.
Чтобы получить выражение для расчета толщины полосы в нейтральном сечении, приравнивают выражения px(hx=h2упр), полученные для пластического и второго упругого участков, получив тем самым уравнение относительно hx=hН.
Его решение дает новую, уточненную формулу толщины полосы в нейтральном сечении, учитывающую все отмеченные выше особенности очага деформации стана горячей прокатки:
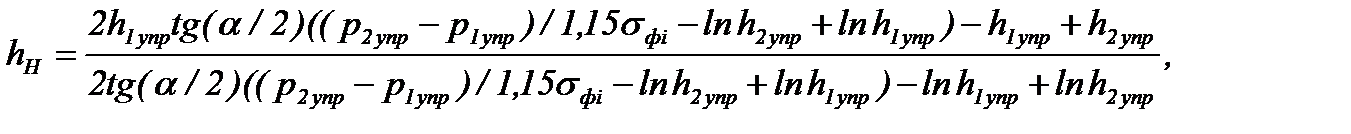 (6.69)
(6.69)
где p2упр – значение нормального контактного напряжения, рассчитанное по уравнению px(hx) для второго упругого участка в сечении hx=h2упр=hi-h2упр.
Относительные упругие деформации по толщине полосы на границах упругих участков с пластическим Δh1упр и Δh2упр вычисляют по формулам, аналогичным выражениям (6.13) и (6.15) (их вывод дан в п. 6.3, б):
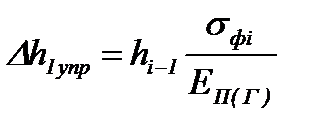 ;
;  (6.70)
(6.70)
Остальные структурные параметры очага деформации, необходимые для расчета px(hx) по формулам таблиц 6.8 и 6.9, вычисляют по тем же формулам, что и при холодной прокатке:
- длина второго упругого участка x2упр – по формуле (6.40), в которой принимают Kпопр=1;
- общая длина первого упругого и пластического участков x1 – по формуле (6.43);
- длина первого упругого участка x1упр – по формуле (6.44);
- длина пластического участка xпл – по формуле (6.45);
- длина зоны опережения пластического участка xпл.опер – по формуле (6.46);
- длина зоны отставания пластического участка xпл.отст – по формуле (6.47);
- общая длина очага деформации i-й рабочей клети lci – по формуле (6.48);
- тангенс угла наклона поверхности AB к оси прокатки tg(α/2) (рис. 6.9) – по формуле (6.50);
- тангенс угла наклона поверхности BC к оси прокатки tgβ (рис. 6.9) – по формуле (6.51).
Дата добавления: 2019-02-08; просмотров: 1827;











