E) Расчет структурных составляющих очага деформации с одним нейтральным сечением

Для дальнейшего расчета необходимо определить толщину полосы в нейтральном сечении указанного варианта очага деформации. С этой целью приравнивают правые части выражений p_{x отст} и p_{x опер}, приведенных в табл. 6.3, подставив в них значение h_x= h_н (т.к. в нейтральном сечении p_{x отст}(h_x= h_н)=p_{x опер}(h_x= h_н)).

В результате этой операции получают алгебраическое уравнение с одной неизвестной величиной h_н. Его решение дает следующую расчетную формулу толщины полосы в нейтральном сечении:

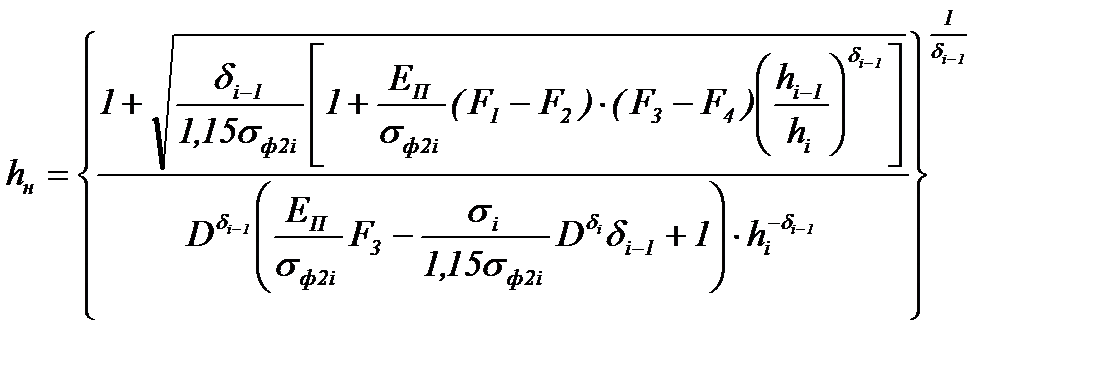(6.39)

где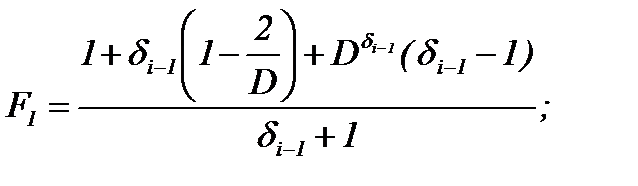

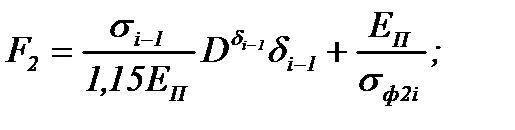
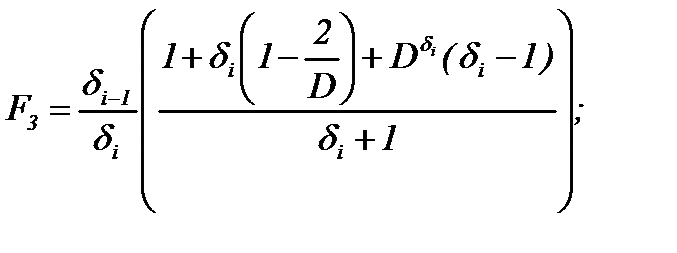
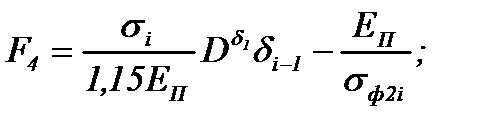
Полученная формула h_н довольно громоздка, она не предназначена для запоминания и ручного расчета (без использования компьютера). Ее основное преимущество в более точном определении величины h_н, чем все другие известные формулы. Учитывая большое значение положения нейтрального сечения в очаге деформации для расчета эффективных технологических режимов прокатки, очень важно как можно точнее определить толщину h_н, а затем – длины всех участков очага деформации.

Используя схему рис. 6.2,а, эти длины следует определять, начиная с величины x_2упр – длины участка упругого восстановления части толщины полосы (второго упругого участка).

В литературе по теории прокатки [1;2;4;6] для расчета длины второго упругого участка очага деформации использована известная в теории упругости формула Герца, определяющая полуширину площадки контакта неподвижного цилиндра с плоскостью, ограничивающей упругое полупространство.

Физические условия контакта вращающихся валков с полосой имеют существенные отличия от условий контакта неподвижного цилиндра с плоскостью: полоса по своим упругим свойствам не адекватна упругому полупространству: ее жесткость зависит от предшествующего наклепа (упрочнения) и толщины, при вращении валка имеет место трение скольжения в контакте с прокатываемой полосой, причем величина коэффициента трения оказывает влияние на длину упругого контакта.

Поэтому для расчета длины x_2упр, рекомендуется, сохранив в качестве основы формулу Герца, ввести в нее поправочный коэффициент K_попрi [25]:

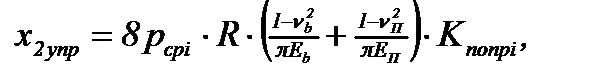(6.40)

где p_ср – среднее значение нормального контактного напряжения p_x в очаге деформации (среднее удельное давление);

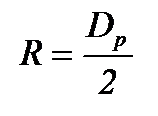- радиус бочки рабочего валка;

ν_В, ν_П, E_В, E_П – упругие константы материалов валков и полосы (их коэф-

фициенты Пуассона и модули упругости).

Для расчета поправочного коэффициента можно использовать регрессионную зависимость его от факторов, не учтенных в формуле Герца: коэффициента трения μ_i (i - номер рабочей клети), наклепа полосы от исходного состояния Δσ_0,2i (приращения предела текучести) и ее толщины h_i [25]:

а) если 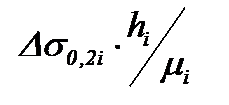≤ 5200 МПа·мм,

K_попрi = 0,718 – 0,00008Δσ_0,2i + 0,821h_i – 146,6μ_i², (6.41)

б) если 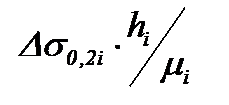> 5200 МПа·мм,

K_попрi=1, т.е. формула Герца дает достоверный результат без поправочного коэффициента.

Чтобы рассчитать x_2упр по формуле (6.40), нужно знать величину p_срi, заранее не известную. Поэтому в качестве первого приближения принимают:

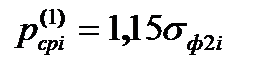, (6.42)

а в дальнейшем величины p_срi и x_2упр уточняют в циклах расчета контактных напряжений методом последовательных приближений (итераций).

После определения x_2упр вычисляют длины остальных участков очага деформации, указанных на схеме рис. 6.2,а:

- общая длина первого упругого и пластического участков:

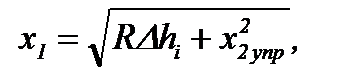(6.43)

где Δh_i=h_i-1-h_i – абсолютное обжатие в i-й рабочей клети;

- длина первого упругого участка:

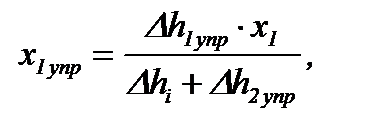(6.44)

где Δh_1упр и Δh_2упр – изменения толщины полосы на первом и втором упругих участках, вычисляемые по формулам (6.13) и (6.15);

- длина пластического участка:

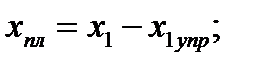(6.45)

- длина зоны опережения пластического участка:

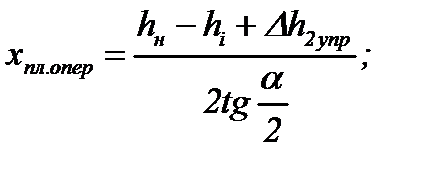(6.46)

- длина зоны отставания пластического участка:

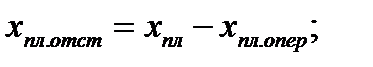(6.47)

- общая длина очага деформации i-ой рабочей клети:

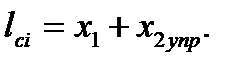(6.48)

Вывод формул (6.43), (6.44) и (6.45) здесь не приводится, чтобы не перегружать материал главы 6, одной из наиболее сложных и объемных в учебнике. Рекомендуем изучающим теорию прокатки вывести эти формулы самостоятельно. Для этого надо рассмотреть отношения между сторонами подобных треугольников ABE и ABF, BCE и BCD, вписанных в окружность бочки валка (см. рис. 6.8) (из выражения, стоящего под знаком квадратного корня, в формуле (6.43), исключены члены, величины которых на 2-3 порядка меньше, чем RΔh и ).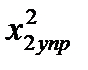

Для последующих расчетов требуется также знать минимальную толщину полосы в очаге деформации, находящуюся в плоскости AFDB. Согласно схеме рис. 6.2,a, она равна:

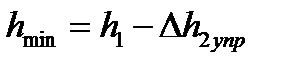(6.49)

(величину Δh_2упр вычисляют по формуле (6.15)).

Кроме того, к структурным параметрам низкого очага деформации относятся углы наклона контактных поверхностей AB и BC к оси прокатки.

Согласно схеме рис. 6.8, угол наклона поверхности AB к оси прокатки равен α/2 (α – угол захвата). Его тангенс равен:

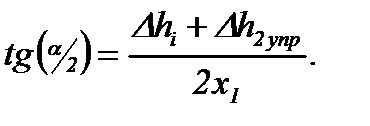(6.50)

(Δh_2упр – см. формулу (6.15), x₁ - см. формулы (6.43), (6.40), (6.41)).

Тангенс угла β наклона поверхности BC к оси прокатки равен:

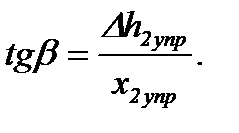(6.51)