Потенциальная энергия деформации

При растяжении

При статическом растяжении образца растягивающая сила F,мед­ленно возрастающая от нуля до какого-то значения, удлиняет образец на величину 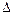l и при этом совершает работу W. Эта работа аккумулируется в деформируемом образце в виде потенциальной энергии деформации U,причем, пренебрегая незначительными потерями энергии (например, теп­ловыми), можно считать, что

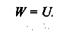
Если диаграмма растяжения построена в координатах (F, 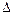l), то, как известно из теоретической механики, площадь диаграммы выражает ра­боту деформации. До предела пропорциональности работа выражается площадью треугольника OAK (см. рис 19.6). Таким образом, потенциаль­ная энергия упругой деформации стержня длиной l постоянного попереч­ного сечения А при одинаковой во всех сечениях продольной силе N = F будет равна

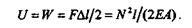
Полная работа, затрачиваемая на разрушение образца, выражается площадью фигуры OABDN диаграммы растяжения, площадь треугольни­ка NDE соответствует работе упругой деформации, исчезающей при раз­рыве образца.

Удельной потенциальной энергией деформации называется работа деформации, приходящаяся на единицу объема бруса:

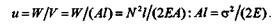
При одновременном действии нескольких растягивающих или сжи­мающих сил и при ступенчатом изменении размеров поперечного сече­ния брус разбивают на отдельные участки, отличающиеся значением на­пряжения; потенциальную энергию деформации всего бруса определяют как сумму потенциальных энергий отдельных участков:

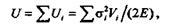
где 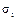— нормальные напряжения в поперечных сечениях на каждом уча­стке;

V_i —объем каждого участка бруса.

Потенциальная энергия деформации выражается в единицах работы — джоулях (Дж), удельная потенциальная энергия — в джоулях на кубический метр (Дж/м³).

Анализируя формулы потенциальной энергии деформации, можно сделать следующие выводы:

1. Потенциальная энергия деформации — величина всегда положи­тельная, так как в ее выражения входят квадраты напряжений или про­дольных сил.

2. По этой причине при вычислении потенциальной энергии де­формации нельзя применять принцип независимости действия сил (из математики известно, что квадрат суммы не равен сумме квадратов слагаемых).