Статически неопределимые задачи
Задачи на расчет конструкций, в элементах которых внутренние силовые факторы не могут быть определены с помощью одних уравнений равновесия статики, называются статически неопределимыми.
Для решения таких задач помимо уравнений равновесия составляют уравнения перемещений или деформаций.
Изменение температуры деталей вызывает изменение их размеров, в результате чего в статически неопределимых системах возникают дополнительные напряжения, называемые температурными.
Рассмотрим невесомый стержень постоянного сечения площадью А,длиной l, жестко защемленный по концам (рис. 19.10). При нагревании в стержне возникнут температурные напряжения сжатия. Определим эти напряжения.
Составим для стержня уравнение равновесия:
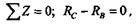
откуда получим, что реакции Rс и RB равны, а, применив метод сечении, установим, что продольная сила N в сечениях стержня равна неизвестным реакциям:
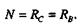
Составим дополнительное уравнение, для чего мысленно отбросим правую заделку и заменим ее реакцией RB, тогда дополнительное уравнение деформаций будет иметь вид
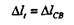
|
(т. е. температурное удлинение стержня равно его укорочению под действием реакции RB, так как связи полагаются абсолютно жесткими).
Температурное удлинение 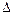 lt =
lt =  tl, где
tl, где  — коэффициент линейного расширения материала стержня; укорочение под действием реакции RB:
— коэффициент линейного расширения материала стержня; укорочение под действием реакции RB: 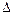 lСВ = RBl /(EA).Приравняем правые части этих равенств:
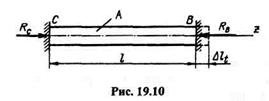
lСВ = RBl /(EA).Приравняем правые части этих равенств:
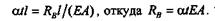
|
|
Определим температурные напряжения:
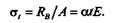
Для того чтобы избежать температурных напряжений, которые могут достигать значительных величин, один конец мостов ставят на катки; в длинных
|
трубопроводах, подвергающихся изменению температуры, делают компенсирующие устройства и т. д.
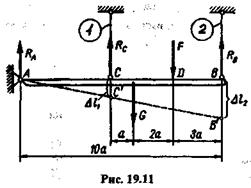
Пример 19.5. Абсолютно жесткая балка, изображенная на рис. 19.11, шарнирно укреплена в стене и подвешена горизонтально на двух шарнирно закрепленных, вертикально расположенных стальных стержнях равной длины l= 2 м. В точке D на балку действует сила F = 20 кН. Площади поперечных сечений стержней равны: А2= 3 см2, А2= б см2. Модуль упругости материала стержней
Е = 2  105 МПа, сила тяжести балки G = 40 кН. Определить напряжения в стержнях 1 и 2.
105 МПа, сила тяжести балки G = 40 кН. Определить напряжения в стержнях 1 и 2.
Решение. Рассматривая равновесие балки, отбросив связи и заменив их реакциями, получаем три неизвестных: реакцию RA шарнира А и реакции RСи RB стержней 1 и 2.
Для данной системы параллельных сил можно составить лишь два уравнения равновесия: уравнение проекций сил на вертикальную ось и уравнение моментов относительно какой-либо точки; следовательно, система статически неопределима.
Для решения задачи необходимо составить дополнительное уравнение перемещений элементов конструкции, для чего изобразим ее в деформированном виде. Из подобия треугольников АСС' и АВВ' получаем
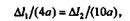
отсюда
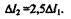
Составим уравнение моментов относительно точки А:
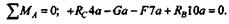
|
Упрощая последнее уравнение, получаем
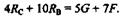
|
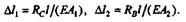
|
По закону Гука
Разделим второе равенство на первое:
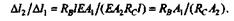
|
 Так как.
Так как.
откуда RВ=5Rс
Находим RВ и RС:
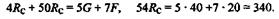

Отсюда
Определяем напряжения 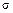 1 и
1 и 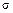 2 в стержнях:
2 в стержнях:
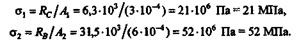
|
Дата добавления: 2021-09-07; просмотров: 476;











