Растяжение под действием

Собственного веса

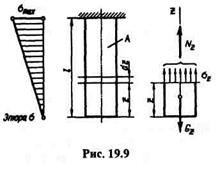
Если ось бруса вертикальна, то собственный вес вызывает деформа­цию растяжения или сжатия. Рассмотрим брус постоянного сечения ве­сом G, длиной l, закрепленный верхним концом и нагруженный только собственным весом G (рис. 19.9).

Для определения напряжений в поперечном сечении на переменном расстоянии z от нижнего конца применим метод сечений. Рассмотрим равновесие нижней части бруса и составим уравнение равновесия:

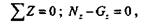
откуда

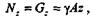
где 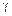— удельный вес материала бруса; А — площадь его попе­речного сечения.

Напряжение

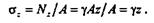
Нормальные напряжения в поперечных сечениях бруса по-200

стоянного сечения, растягиваемого лишь собственным весом, прямо пропорциональны расстоянию сечения от нижнего конца и не зависят от площади сечения.

Очевидно, что опасное сечение бруса будет находиться в заделке:

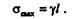
Эпюра распределения нормальных напряжений вдоль оси бруса представляет собой треугольник (см. рис. 19.9).

Определим длину бруса постоянного сечения, при которой напряже­ние только от собственного веса достигает допускаемого и брус не может нести полезной нагрузки. Такая длина бруса называется предельной:

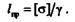
Если 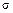_шах станет равным пределу прочности, то брус разрушится от собственного веса. Длина бруса, при которой он разрушается под дейст­вием собственного веса, называется критической:

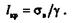
Как видно из формул, предельная и критическая длины не зависят от площади поперечного сечения бруса.

Вычислим для примера критическую длину бруса из стали Ст2, у ко­торой 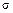_в= 360 МПа, а удельная сила тяжести 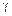= 7,85 10⁴ Н/м²:

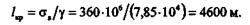
Определим удлинение 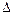l бруса под действием собственного веса, для чего выделим бесконечно малый элемент длиной dz. Ввиду малости дли­ны элемента будем считать, что в его пределах продольная сила N_z не из­меняется. Применив закон Гука, получим

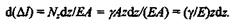
Проинтегрировав это выражение в пределах от 0 до l, получим

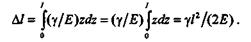
Так как

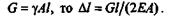
Удлинение бруса постоянного сечения под действием собственного веса в 2 раза меньше удлинения при растяжении силой, равной собст­венному весу и приложенной к концу бруса.