Произвольно расположенных сил к данному центру

Приведением системы сил называется замена ее другой систе­мой, эквивалентной первой, но более простой.

Теорема.Плоская сис­тема произвольно располо­женных сил в общем случае эквивалентна одной силе, приложенной в центре при­ведения, и одной паре.

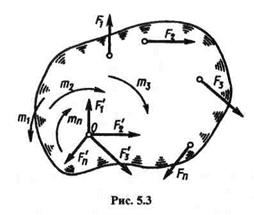
Пусть дана плоская сис­тема п произвольно распо­ложенных сил (F₁, F₂, F₃, ..., F_п-1, F_п). Перенесем парал­лельно все силы в произволь­но выбранный в плоскости действия сил центр приведе­ния О, добавив при этом п пар (рис. 5.3). Моменты этих пар т₁, т₂, т₃, ..., т_п,равны моментам данных сил относительно центра приведения О.

Вместо заданной системы п произвольно расположенных сил мы по­лучили систему и сил, приложенных в центре приведения, равных дан­ным силам по модулю и одинаковых с ними по направлению, и систему п присоединенных пар:

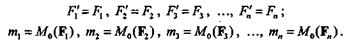
Эта новая система эквивалентна данной.

Плоская система сил, приложенных в одной точке, эквивалентна од­ной силе, которая равна векторной сумме этих сил и приложена в той же точке, следовательно,

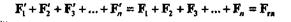
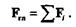
или

Эту силу назовем главным вектором данной системы. Глав­ный вектор плоской системы произвольно расположенных сил равен векторной сумме всех сил системы и приложен в центре приведения.

Графически главный вектор выражается замыкающей стороной си­лового многоугольника, построенного на данных силах. Аналитически модуль главного вектора можно вычислить по формуле

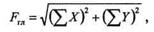
а направляющий косинус — по формуле

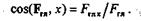
Плоская система пар эквивалентна одной паре, момент которой ра­вен алгебраической сумме моментов данных пар, следовательно,

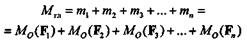
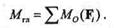
или

Эту пару с моментом М_глназовем главным моментом задан­ной системы сил.

Главный момент плоской системы произвольно расположенных сил равен алгебраической сумме моментов всех сил системы относительно центра приведения.

Таким образом, всякая плоская система сил в общем случае эквива­лентна системе, состоящей из силы и пары сил, следовательно, теорема доказана.

Не следует считать, что главный вектор и главный момент имеют чисто формальное значение, введенное для удобства доказательства, и что их можно найти только с помощью вычислений. Нередко отдельно действующие на тело силы определить трудно или невозможно, а глав­ный вектор или главный момент этих сил найти сравнительно легко. Так, например, число точек контакта и модули сил трения между вращающим­ся валом и подшипником скольжения, как правило, неизвестны, но глав­ный момент этих сил можно определить простым измерением; второй пример: в характеристику электродвигателя входит не сила, с которой статор действует на ротор, а вращающий момент.