Свойства главного вектора

И главного момента

Свойства главного вектора и главного момента заключаются в сле­дующем:

1) модуль и направление главного вектора данной системы не зави­сят от выбора центра приведения, так как при любом центре приведения силовой многоугольник, построенный на данных силах, будет один и тот же;

2) величина и знак главного момента в общем случае зависят от вы­бора центра приведения (кроме одного случая, о котором будет сказано в § 5.4), так как при перемене центра приведения меняются плечи сил, а модули их остаются неизменными;

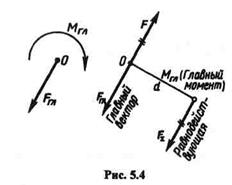
3) главный вектор и равно­действующая системы сил векторно равны, но в общем случае не эквивалентны. Пусть извест­ны главный вектор F_гл и глав­ный момент М_гл какой-то пло­ской системы сил (рис.5.4).Оп­ределим равнодействующую этой системы.

Пользуясь известным свой­ством пары сил, преобразуем главный момент М_глтак, чтобы

силы пары F и F 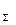- были параллельны и по модулю равны главному век­тору F _гл:

причем сила F приложена к точке О противоположно F _гл.

Далее систему (F _гл, F), как взаимно уравновешенную, отбросим:

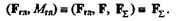
В результате получили одну силу F 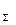эквивалентную главному век­тору и главному моменту, т. е. равнодействующую системы, причем

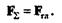
Модуль равнодействующей

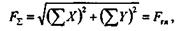
а положение линии действия равнодействующей определяется плечом d по формуле

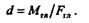
В результате можно считать установленным, что главный вектор и равнодействующая векторно равны, но не эквивалентны;

4) главный вектор и равнодействующая эквивалентны лишь в част­ном случае, когда главный момент системы равен нулю; последнее воз­можно в случае, когда центр приведения находится на линии действия равнодействующей.

Из рис 5.4 видно, что момент равнодействующей F 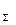- относительно

центра приведения О равен моменту М_гл пары (F , F), т. е. главному мо­менту данной системы:

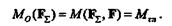
Так как М_гл = 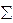M₀(F_i), а за центр приведения можно взять любую точку плоскости действия сил данной системы, то всегда имеем

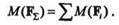
Полученная формула является математическим выражением теоремы о моменте равнодействующей.

Теорема.Момент равнодействующей силы относительно какой-либо точки, расположенной в плоскости действия сил, равен алгебраиче­ской сумме моментов составляющих сил относительно той же точки.

Теорему о моменте равнодействующей впервые доказал француз­ский ученый Вариньон (1654—1722), поэтому ее называют теоремой Вариньона.

Применим доказанную теорему для определения положения линии действия равнодействующей F 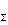плоской системы п параллельных сил:

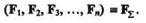
Выберем какую-либо точку О плоскости действия сил за центр мо­ментов и согласно теореме Вариньона запишем

где d —плечо равнодействующей F 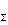относительно точки О.

Из последнего равенства определяем плечо d:

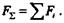так как, согласно § 3.2,

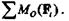Чтобы установить, в какую сторону от точки О следует на перпенди­куляре к линиям действия сил отложить плечо d, следует учесть, во-первых, направление вектора F 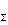и, во-вторых, знак