Лемма о параллельном переносе силы

Лемма.Механическое состояние твердого тела не нарушится, если данную силу перенести параллельно первоначальному положению в про-

извольную точку тела, добавив при этом пару, момент которой равен моменту данной силы относительно новой точки приложения.

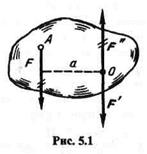
Возьмем тело, находящееся под действием некоторой системы сил, в числе которых есть сила F, приложенная в точке А (рис. 5.1). Выберем произвольную точку О,которую назовем центром приведения, и на основании аксиомы IV приложим в этой точке две равные силы F' и F", параллельные данной силе F, причем

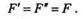
Систему сил (F, F', F"), эквивалентную силе F, представим как силу F, перенесенную параллельно первоначальному положению в произволь­но выбранный центр приведения О,и пару (F, F"), момент которой равен моменту данной силы относительно центра приведения О,являющегося новой точкой приложения силы:

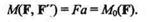
Лемма доказана.

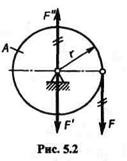
Описанный выше перенос силы можно показать на примере. Рас­смотрим колесо А радиуса г, вращающееся на оси в подшипниках (рис. 5.2). Пусть к ободу колеса по касательной приложена сила F (такую силу на­зывают окружной).

Для определения действия силы F на колесо и подшипники приме­ним доказанную лемму и перенесем эту силу параллельно самой себе на ось колеса. В результате получим силу F' = F, вызывающую давление на подшипники, и пару сил (F, F") с моментом, равным Fr, которая будет вращать колесо.