Теорема о сложении пар
Теорема.Всякая плоская система пар эквивалентна одной результирующей паре, момент которой равен алгебраической сумме моментов данных пар.
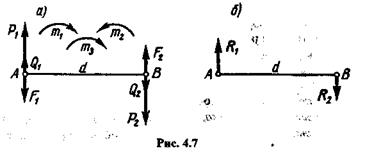
Пусть даны три пары с моментами т1, т2, m3, действующие в одной плоскости (рис. 4.7, а).
На основании следствия из теоремы об эквивалентных парах преобразуем эти пары так, чтобы их плечи стали равными d,и перенесем к произвольно взятому на плоскости отрезку АВ длиной d.
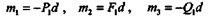
|
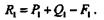
|
| Тогда вместо заданной системы пар получим новую систему, эквивалентную данной, причем моменты данных и новых пар будут равны, т. е. |
| Сложив три силы в точке А,получим равнодействующую R1 (рис. 4.1, б), модуль которой |
Сложив три силы в точке В,получим равнодействующую R2, модуль которой
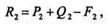
причем очевидно, что силы R1 и R2 равны по модулю, параллельны и противоположно направлены.
Значит, система (R1, R2) представляет собой пару с плечом d, эквивалентную данной системе пар.
Момент этой результирующей пары
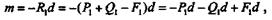
или
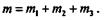
Аналогичное доказательство можно привести для любой плоской системы пар, т. е. в общем виде можно записать
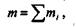
что и требовалось доказать.
Дата добавления: 2021-09-07; просмотров: 490;











